题目内容

【题目】在一场足球比赛中，一球员从球门正前方10米处起脚射门，当球飞行的水平距离为6米时达到最高点，此时球高为3米．

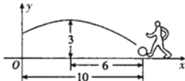
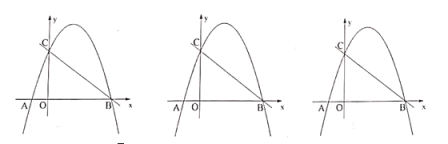
（1）如图建立直角坐标系，当球飞行的路线为一抛物线时，求此抛物线的解析式．

（2）已知球门高为2.44米，问此球能否射中球门（不计其它情况）．

【答案】（1）y＝﹣（x﹣4）2+3；（2）能射中球门．

【解析】

（1）根据条件可以得到抛物线的顶点坐标是（4，3），利用待定系数法即可求得函数的解析式；

（2）求出当x＝0时，抛物线的函数值，与2.44米进行比较即可判断．

（1）抛物线的顶点坐标是（4，3），

设抛物线的解析式是：y＝a（x﹣4）2+3，

把（10，0）代入得36a+3＝0，

解得a＝-，

则抛物线是y＝﹣（x﹣4）2+3；

（2）当x＝0时，y＝-×16+3＝3﹣＝＜2.44米．

故能射中球门．

练习册系列答案
相关题目

【题目】如图，已知点A，点C在反比例函数y＝（k＞0，x＞0）的图象上，AB⊥x轴于点B，OC交AB于点D，若CD＝OD，则△AOD与△BCD的面积比为__．

【题目】我市某企业承接了上海世博会的礼品盒制作业务，他们购得规格是170cm×40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材．如图1所示，（单位：cm）

（1）列出方程（组），求出图甲中a与b的值．

（2）若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图2的竖式与横式两种无盖礼品盒．

①两种裁法共产生A型板材　 　张，B型板材　 　张；

②做成的竖式和横式两种无盖礼品盒总数最多是多少个？此时横式无盖礼品盒可以做多少个？

【题目】如图，抛物线与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).

（1）求直线AB的函数关系式；

（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；

（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由

【题目】如图，已知直线与轴交于点，与轴交于点，抛物线经过、两点并与轴的另一个交点为，且.

（1）求抛物线的解析式；

（2）点为直线上方对称轴右侧抛物线上一点，当的面积为时，求点的坐标；

（3）在（2）的条件下，连接，作轴于，连接、，点为线段上一点，点为线段上一点，满足，过点作交轴于点，连接，当时，求的长.

【题目】在平面直角坐标系中，二次函数y＝﹣x2+2x+3的图象交x轴于点A、B（点A在点B的左侧）．若把点B向上平移m（m＞0）个单位长度得点B1，若点B1向左平移n（n＞0）个单位长度，将与该二次函数图象上的点B2重合；若点B1向左平移（n+2）个单位长度，将与该二次函数图象上的点B3重合．则n的值为（　　）

A.1B.2C.3D.4

【题目】如图（1）已知矩形AOCD在平面直角坐标系xOy中，∠CAO＝60°，OA＝2，B点的坐标为（2，0），动点M以每秒2个单位长度的速度沿A→C→B运动（M点不与点A、点B重合），设运动时间为t秒．

（1）求经过B、C、D三点的抛物线解析式；

（2）点P在（1）中的抛物线上，当M为AC中点时，若△PAM≌△PDM，求点P的坐标；

（3）当点M在CB上运动时，如图（2）过点M作ME⊥AD，MF⊥x轴，垂足分别为E、F，设矩形AEMF与△ABC重叠部分面积为S，求S与t的函数关系式，并求出S的最大值；

（4）如图（3）点P在（1）中的抛物线上，Q是CA延长线上的一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，求点P的坐标．

【题目】如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是的中点，则下列结论：①OC∥AE；②EC＝BC；③∠DAE＝∠ABE；④AC⊥OE，其中正确的有（　　）

A.1个B.2个C.3个D.4个

【题目】如图，△ABC中，AB＝AC＝5，BC＝6，点D、E分别是边AB、AC上的动点（点D、E不与△ABC的顶点重合），AD和BE交于点F，且∠AFE＝∠ABC

（1）求证：△ABD∽△BCE；

（2）设AE＝x，ADFD＝y，求y关于x的函数关系式，并直接写出x的取值范围；

（3）当△AEF是等腰三角形时，求DF的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网