题目内容
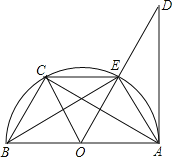
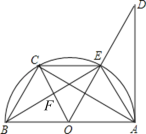
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由C为弧EB中点,利用垂径定理的逆定理得到OC垂直于BE,根据等弧对等弦得到BC=EC,再由AB为直角,利用圆周角定理得到AE垂直于BE,进而得到一对直角相等,利用同位角相等两直线平行得到OC与AE平行,由AD为圆的切线,利用切线的性质得到AB与DA垂直,利用同角的余角相等得到∠DAE=∠ABE,根据E不一定为弧AC中点,可得出AC与OE不一定垂直,即可确定出结论成立的序号.
解:∵C为![]() 的中点,即
的中点,即![]() ,
,
∴OC⊥BE,BC=EC,选项②正确;
设AE与CO交于F,∴∠BFO=90°,
∵AB为圆O的直径,
∴AE⊥BE,即∠BEA=90°,
∴∠BFO=∠BEA,
∴OC∥AE,选项①正确;
∵AD为圆的切线,
∴∠DAB=90°,即∠DAE+∠EAB=90°,
∵∠EAB+∠ABE=90°,
∴∠DAE=∠ABE,选项③正确;
点E不一定为![]() 中点,故E不一定是
中点,故E不一定是![]() 中点,选项④错误,
中点,选项④错误,
则结论成立的是①②③,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目