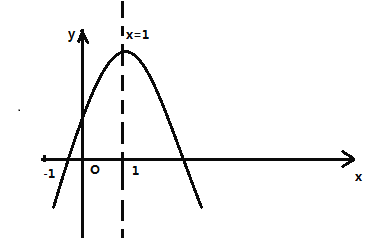题目内容
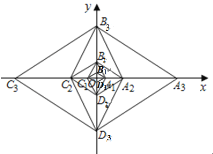
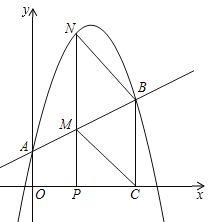
【题目】如图,抛物线![]() 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由
【答案】(1)![]() ;(2)
;(2)![]() (0≤t≤3);(3)t=1或2时;四边形BCMN为平行四边形;t=1时,平行四边形BCMN是菱形,t=2时,平行四边形BCMN不是菱形,理由见解析.
(0≤t≤3);(3)t=1或2时;四边形BCMN为平行四边形;t=1时,平行四边形BCMN是菱形,t=2时,平行四边形BCMN不是菱形,理由见解析.
【解析】
(1)由A、B在抛物线上,可求出A、B点的坐标,从而用待定系数法求出直线AB的函数关系式.
(2)用t表示P、M、N 的坐标,由等式![]() 得到函数关系式.
得到函数关系式.
(3)由平行四边形对边相等的性质得到等式,求出t.再讨论邻边是否相等.
解:(1)x=0时,y=1,
∴点A的坐标为:(0,1),
∵BC⊥x轴,垂足为点C(3,0),
∴点B的横坐标为3,
当x=3时,y=![]() ,
,
∴点B的坐标为(3,![]() ),
),
设直线AB的函数关系式为y=kx+b,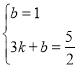 ,
,
解得,![]() ,
,
则直线AB的函数关系式![]()
(2)当x=t时,y=![]() t+1,
t+1,
∴点M的坐标为(t,![]() t+1),
t+1),
当x=t时,![]()
∴点N的坐标为![]()
![]() (0≤t≤3);
(0≤t≤3);
(3)若四边形BCMN为平行四边形,则有MN=BC,
∴![]() ,
,
解得t1=1,t2=2,
∴当t=1或2时,四边形BCMN为平行四边形,
①当t=1时,MP=![]() ,PC=2,
,PC=2,
∴MC=![]() =MN,此时四边形BCMN为菱形,
=MN,此时四边形BCMN为菱形,
②当t=2时,MP=2,PC=1,
∴MC=![]() ≠MN,此时四边形BCMN不是菱形.
≠MN,此时四边形BCMN不是菱形.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.