Question

【题目】如图，已知直线与轴交于点，与轴交于点，抛物线经过、两点并与轴的另一个交点为，且.

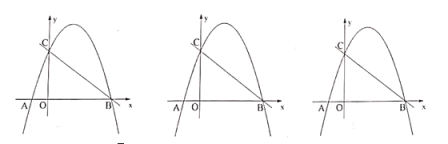
（1）求抛物线的解析式；

（2）点为直线上方对称轴右侧抛物线上一点，当的面积为时，求点的坐标；

（3）在（2）的条件下，连接，作轴于，连接、，点为线段上一点，点为线段上一点，满足，过点作交轴于点，连接，当时，求的长.

Answer 1

【答案】（1）；（2）R（3，3）；（3）1或．

【解析】

（1）求出A、B、C的坐标，把A、B的坐标代入抛物线解析式，解方程组即可得出结论；

（2）设R（t，）．作RK⊥y轴于K，RW⊥x轴于W，连接OR．

根据计算即可；

（3）在RH上截取RM=OA，连接CM、AM，AM交PE于G，作QF⊥OB于H．分两种情况讨论：①点E在F的左边；②点E在F的右边．

（1）当x=0时y=3，

∴C（0，3），

∴OC=3．

∵OC=3OA，

∴OA=1，

∴A（-1，0）．

当y=0时x=4，

∴B（4，0）．

把A、B坐标代入得解得：，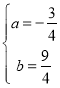

∴抛物线的解析式为．

（2）设R（t，）．

作RK⊥y轴于K，RW⊥x轴于W，连接OR．

∵

∵，

∴，（舍去），，

∴R（3，3）．

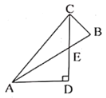
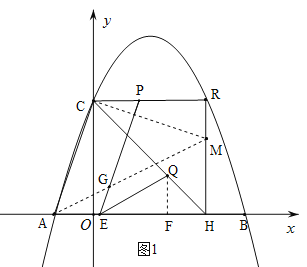
（3）在RH上截取RM=OA，连接CM、AM，AM交PE于G，作QF⊥OB于H．

分两种情况讨论：①当点E在F的左边时，如图1．

∵CR=CO，∠CRM=∠COA，

∴△CRM≌△COA，

∴CM=CA，∠RCM=∠OCA，

∴∠ACM=∠OCR=90°，

∴∠CAM=∠CMA=45°．

∵AC∥PE，

∴∠CAM=∠AGE=45°．

∵∠PEQ=45°，

∴∠AGE=∠PEQ，

∴AM∥EQ，

∴∠MAH=∠QEF．

∵∠QFE=∠MHA=90°，

∴△QEF∽△MAH，

∴．

∵OA=1，OH=3，MH=RH-RM=3-1=2，

∴AH=AO+OH=4，

∴EF=2QF．

设CP=m，

∴QH=CP=m．

∵OC=OH，

∴∠OHC=45°，

∴QF=FH=m，

∴EF=2m，

∴EH=3m．

∵ACPE为平行四边形，

∴AE=CP=m．

∵EH=AH-AE=4-m，

∴3m=4-m，

∴m=1，

∴CP=1．

②当点E在F的右边时，设AM交QE于N．如图2．

∵CR=CO，∠CRM=∠COA，

∴△CRM≌△COA，

∴CM=CA，∠RCM=∠OCA，

∴∠ACM=∠OCR=90°，

∴∠CAM=∠CMA=45°．

∵AC∥PE，

∴∠CAM=∠AGE=45°．

∵∠PEQ=45°，

∴∠AGE=∠PEQ=45°，

∴∠ENG=∠ENA=90°．

∵∠EQF+∠QEF=90°，∠EAN+∠QEF=90°，

∴∠EQF=∠MAB．

∵∠QFE=∠AHM=90°，

∴△QEF∽△AMH，

∴，

∴QF=2EF．

设CP=m，

∴QH=CP=m．

∵OC=OH，

∴∠OHC=45°，

∴QF=FH=m，

∴EF=m，

∴EH=m．

∵ACPE为平行四边形，

∴AE=CP=m．

∵EH=AH-AE=4-m，

∴4-m=m，

∴m=，

∴CP=．

综上所述：CP的值为1或．