Question

【题目】如图，△ABC中，AB＝AC＝5，BC＝6，点D、E分别是边AB、AC上的动点（点D、E不与△ABC的顶点重合），AD和BE交于点F，且∠AFE＝∠ABC

（1）求证：△ABD∽△BCE；

（2）设AE＝x，ADFD＝y，求y关于x的函数关系式，并直接写出x的取值范围；

（3）当△AEF是等腰三角形时，求DF的长度．

Answer 1

【答案】（1）证明见解析；（2）；（3）或．

【解析】

（1）根据两个角对应相等的两个三角形相似证明即可．

（2）由△BDF∽△ADB，可得＝，推出BD2＝DFAD，由△ABD∽△BCE，可得＝，结论＝，推出BD＝（5x），由此即可解决问题．

（3）分两种情形：①如图1中，当AE＝EF时，②如图2中，当FA＝FE时，作AH⊥BC于H，利用相似三角形的性质分别求解即可解决问题．

（1）证明：∵∠AFE＝∠ABC，∠AFE＝∠ABF+∠BAF，∠ABC＝∠ABF+∠CBE，

∴∠BAD＝∠CBE，

∵AB＝AC，

∴∠ABD＝∠C，

∴△ABD∽△BCE．

（2）解：∵∠BDF＝∠ADB，∠DBF＝∠BAD，

∴△BDF∽△ADB，

∴＝，

∴BD2＝DFAD，

∵△ABD∽△BCE，

∴＝，

∴＝，

∴BD＝（5﹣x），

∴y＝ADDF＝BD2＝（5﹣x）2

∴．/p>

（3）解：①如图1中，当AE＝EF时，

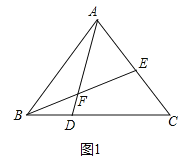
∵AE＝EF，

∴∠AFE＝∠EAF，

∵∠AFE＝∠ABC＝∠C，

∴△DCA∽△ABC∽EAF，

∴＝，

∴＝，

∴AD＝DC＝，同法可得AF＝x，

∴BD＝6﹣＝，

∵BD2＝DFDA，

∴＝DF，

∴DF＝．

②如图2中，当FA＝FE时，作AH⊥BC于H．

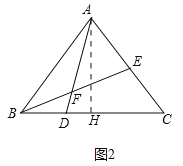
∵FA＝FE，

∴∠FAE＝∠FEA，

∵△ABD∽∠BCE，

∴∠ADB＝∠BEC，

∴∠ADC＝∠FEA，

∴∠CDA＝∠CAD，

∴CD＝CA＝5，

∵AB＝AC，AH⊥BC，

∴BH＝CH＝3，

∴AH＝＝4，

∴DH＝5﹣3＝2，AD＝＝＝2，

∵BD＝1，BD2＝DFAD，

∴1＝DF2，

∴DF＝．

综上所述，DF的长是或．