题目内容
【题目】已知△ABC中,AB=AC.
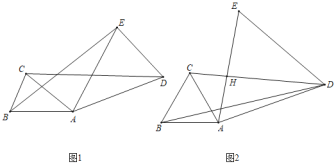
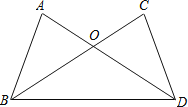
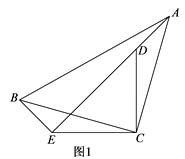
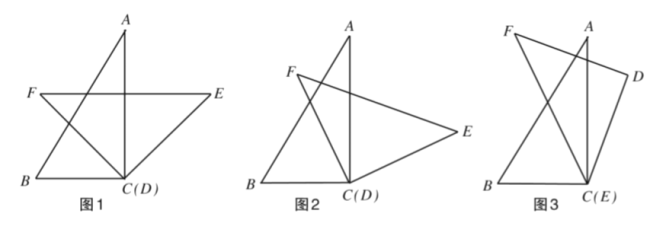
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
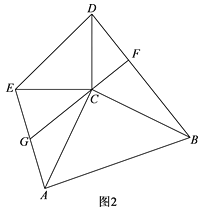
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
【答案】(1)详见解析;(2)BD=10.
【解析】
(1)根据SAS证明△BAE和△CAD全等,再利用全等三角形的性质证明即可;
(2)根据等边三角形的性质和含30°的直角三角形的性质解答即可.
解:(1)∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
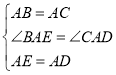 ,
,
∴△BAE≌△CAD(SAS),
∴CD=BE;
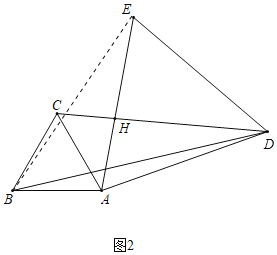
(2)解:连接BE,如图2所示:
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∵CD垂直平分AE,
∴∠CDA=![]() ∠ADE=
∠ADE=![]() ×60°=30°,
×60°=30°,
∵△BAE≌△CAD,
∴BE=CD=8,∠BEA=∠CDA=30°,
∴BE⊥DE,
DE=AD=6,
∴BD=![]() =10.
=10.

 阅读快车系列答案
阅读快车系列答案【题目】解决问题:(假设行车过程没有停车等时,且平均车速为0.5千米/分钟)
华夏专车 | 神州专车 | |
里程费 | 1.8元/千米 | 2元/千米 |
时长费 | 0.3元/分钟 | 0.6元/分钟 |
远途费 | 0.8元/千米产(超过7千米部分) | 无 |
起步价 | 无 | 10元 |
华夏专车:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出的部分按每千米加收0.8元. 神州专车:车费由里程费、时长费、起步价三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;起步价与行车距离无关. | ||
(1)小明在该地区出差,乘车距离为10千米,如果小明使用华夏专车,需要支付的打车费用为 元;
(2)小强在该地区从甲地乘坐神州专车到乙地,一共花费42元,求甲乙两地距离是多少千米?
(3)神州专车为了和华夏专车竞争客户,分别推出了优惠方式,华夏专车对于乘车路程在7千米以上(含7千米)的客户每次收费立减9元;神州打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.