��Ŀ����
����Ŀ��������⣺(�����г�����û��ͣ����ʱ����ƽ������Ϊ0��5ǧ��/����)
����ר�� | ����ר�� | |
��̷� | 1.8Ԫ/ǧ�� | 2Ԫ/ǧ�� |
ʱ���� | 0.3Ԫ/���� | 0.6Ԫ/���� |
Զ;�� | 0.8Ԫ/ǧ�ײ�������7ǧ�ײ��֣� | �� |
�� | �� | 10Ԫ |
����ר������������̷ѡ�ʱ���ѡ�Զ;�������ֹ��ɣ�������̷Ѱ��г���ʵ����̼��㣻ʱ���Ѱ��г���ʵ��ʱ����㣻Զ;�ѵ���ȡ��ʽΪ���г����7ǧ�����ڣ���7ǧ�ף�����Զ;�ѣ�����7ǧ�ģ������IJ��ְ�ÿǧ����0.8Ԫ�� ����ר������������̷ѡ�ʱ���ѡ��������ֹ��ɣ�������̷Ѱ��г���ʵ����̼��㣻ʱ���Ѱ��г���ʵ��ʱ����㣻�����г������أ� | ||
��1��С���ڸõ�������˳�����Ϊ10ǧ�ף����С��ʹ�û���ר������Ҫ֧���Ĵ���Ϊ Ԫ��
��2��Сǿ�ڸõ����Ӽس�������ר�����ҵأ�һ������42Ԫ����������ؾ����Ƕ���ǧ�ף�
��3������ר��Ϊ�˺ͻ���ר�������ͻ����ֱ��Ƴ����Żݷ�ʽ������ר�����ڳ˳�·����7ǧ������(��7ǧ��)�Ŀͻ�ÿ���շ�����9Ԫ�����ݴ���5���Żݣ��Բ�����һ�ִ�ʽ�����������Ľ��飮
���𰸡���1��26.4��(2) 10ǧ�ף�(3) ������7ǧ��12.25ǧ��֮��ʱ������ר�������㣻������12.25ǧ��ʱ��һ�����㣻�����ڴ���12.25ǧ��֮��ʱ������ר�������㣮
��������
��1�����ݻ���ר���ij��Ѽ��㷽��������⣻
(2)��������ؾ���Ϊxǧ��,���������г�һԪһ�η��̼�����⣻
(3)��˳�·��Ϊaǧ��,��������ֱ��ʾ�����ֳ˳���ʽ�ķ��ã��Ƚϼ�����⣮
��1��С���ڸõ�������˳�����Ϊ10ǧ�ף�
ʱ��Ϊ10��0.5=20�����ӣ�
��ʹ�û���ר������Ҫ֧���Ĵ���Ϊ1.8��10+0.3��20+��10-7����0.8=26.4Ԫ��
�ʴ�Ϊ��26.4��
(2) ��������ؾ���Ϊxǧ��,���������
10+2x+0.6��![]() =42
=42
���x=10��
��������ؾ�����10ǧ�ף�
(3)��˳�·��Ϊaǧ�ף�a��7��
���ר���ķ���Ϊ��![]() =3.2a-14.6��
=3.2a-14.6��
����ר���ķ���Ϊ��0.5����![]() ��=1.6a+5��
��=1.6a+5��
��3.2a-14.6=1.6a+5
���a=12.25
��7��a��12.25ʱ������ר�������㣻
a=12.25��һ�����㣻
a��12.25ʱ������ר������
��������7ǧ��12.25ǧ��֮��ʱ������ר�������㣻������12.25ǧ��ʱ��һ�����㣻�����ڴ���12.25ǧ��֮��ʱ������ר�������㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
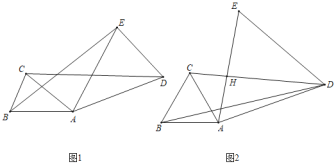
Сѧ��10����Ӧ����ϵ�д�����Ŀ����ͼ������ABC�У���ACB=90�㣬��A=30�㣬AB=6cm����D���߶�AB��һ���㣬���߶�CD�Ƶ�C��ʱ����ת50����CD�䣬����BD�䣮��ADΪxcm��BD��Ϊycm��
С�ĸ���ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽��.
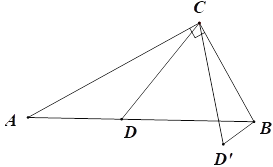
������С�ĵ�̽�����̣��벹��������
(1)ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
|
| 1 | 2 | 3 | 3.5 | 4 | 5 | 6 |
| 3.5 | 1.5 | 0.5 | 0.2 | 0.6 | 1.5 | 2.5 |
��˵������ȫ����ʱ�����ֵ����һλС����
(2)����ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ����

(3)��ϻ����ĺ���ͼ������⣺��BD=BD'ʱ���߶�AD�ij���ԼΪ_________![]() .
.