题目内容
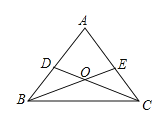
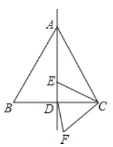
【题目】如图，边长为4的等边三角形ABC中，E是对称轴AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF，则在点E运动过程中，DF的最小值是______.
【答案】1
【解析】
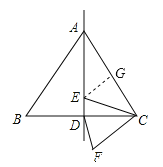
取AC的中点G，连接EG，根据等边三角形的性质可得CD=CG，再求出∠DCF=∠GCE，根据旋转的性质可得CE=CF，然后利用“边角边”证明△DCF和△GCE全等，再根据全等三角形对应边相等可得DF=EG，然后根据垂线段最短可得EG⊥AD时最短，再根据∠CAD=30°求解即可．
解：如图，取AC的中点G，连接EG，
∵旋转角为60°，
∴∠ECD+∠DCF=60°，
又∵∠ECD+∠GCE=∠ACB=60°，
∴∠DCF=∠GCE，
∵AD是等边△ABC的对称轴，
，
∴CD=CG，
又∵CE旋转到CF，
∴CE=CF，
在△DCF和△GCE中，
，
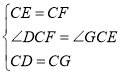∴△DCF≌△GCE（SAS），
∴DF=EG，
根据垂线段最短，EG⊥AD时，EG最短，即DF最短，
此时
，
，
∴DF=1.
故答案为：1.
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
【题目】某中学为了科学建设“学生健康成长工程”．随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗？”的问卷调查，将回收的问卷进行分析整理，得到了如下的样本统计表和扇形统计图：
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
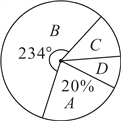
（1）求
的值；
（2）该校学生家庭总数为500，学校决定按比例在
类家庭中抽取家长组成培训班，其比例为
类取20%，
类各取60%，请你估计该培训班的家庭数；
（3）若在
类家庭中只有一个城镇家庭，其余是农村家庭，请用列举法求出在类中随机抽出2个家庭进行深度采访，其中有一个是城镇家庭的概率．
