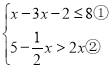题目内容
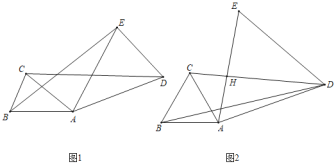
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
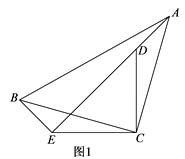
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
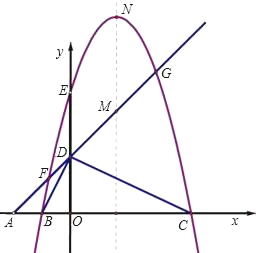
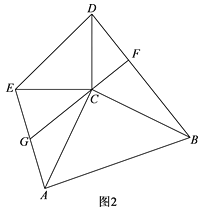
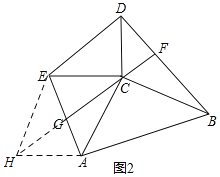
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】(1)根据旋转的性质,得到∠ADC=∠BEC=135°,进而得到∠AEB=90°,再根据勾股定理以及AD的长,即可得出DE=7,最后根据等腰Rt△CDE,运用勾股定理得到CD的长;
(2)过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,再根据∠BCD+∠ACE=180°,即可得到∠CAE=∠BCD,再判定△BCD≌△CAH(ASA),得出AH=CD=CE,BD=CH,再判定四边形ACEH是平行四边形,即可得到CH=2CG,进而得出BD=2CG.
(1)如图1,
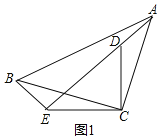
∵△ADC是由△BEC绕点C旋转得到的,
∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=![]() ,∠EDC=∠DEC=45°,
,∠EDC=∠DEC=45°,
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=![]() =12,
=12,
∴DE=7,
∴等腰Rt△CDE中,CD=![]() DE=
DE=![]() ;
;
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
∵∠ACB=∠DCE=90°,
∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
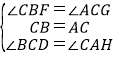 ,
,
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.

 ABC考王全优卷系列答案
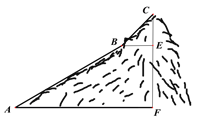
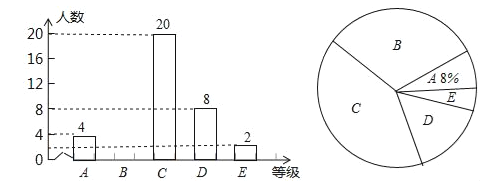
ABC考王全优卷系列答案【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
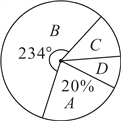
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.