题目内容
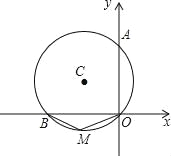
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点.
的中点.
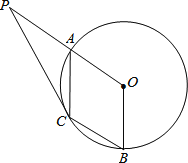
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为![]() ,求BC长.
,求BC长.
【答案】(1)四边形OACB是菱形,见解析;(2)3
【解析】
(1)首先连接OC,由A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点,易证得△AOC与△BOC都是等边三角形,则可得AC=OA=OC=OB=BC,继而证得四边形OACB是菱形.
的中点,易证得△AOC与△BOC都是等边三角形,则可得AC=OA=OC=OB=BC,继而证得四边形OACB是菱形.
(2)由AP=OA,易证得△OPC是直角三角形,然后利用勾股定理求得答案.
解:(1)四边形OACB是菱形.
理由:连接OC,
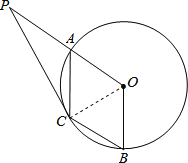
∵∠AOB=120°,C是劣弧![]() 的中点,
的中点,
∴∠AOC=∠BOC=![]() ∠AOB=60°,
∠AOB=60°,
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=![]() ∠OAC=30°,
∠OAC=30°,
∴∠OCP=90°,
设圆O的半径为x,则OC=x,OP=2x
∴![]() ,
,
∴x=3
∵四边形OACB是菱形.
∴BC=3

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目