Question

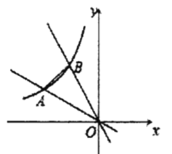
【题目】如图，在平面直角坐标系中，O为坐标原点，△AOB是等腰直角三角形，∠AOB=90°，点A（2,1）.

（1）求点B的坐标；

（2）求经过A、O、B三点的抛物线的函数表达式；

（3）在（2）所求的抛物线上，是否存在一点P，使四边形ABOP的面积最大？若存在，求出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】(1) B（-1.2）;(2) y=;(3)见解析.

【解析】

（1）过A作AC⊥x轴于点C，过B作BD⊥x轴于点D，则可证明△ACO≌△ODB，则可求得OD和BD的长，可求得B点坐标；

（2）根据A、B、O三点的坐标，利用待定系数法可求得抛物线解析式；

（3）由四边形ABOP可知点P在线段AO的下方，过P作PE∥y轴交线段OA于点E，可求得直线OA解析式，设出P点坐标，则可表示出E点坐标，可表示出PE的长，进一步表示出△POA的面积，则可得到四边形ABOP的面积，再利用二次函数的性质可求得其面积最大时P点的坐标．

（1）如图1，过A作AC⊥x轴于点C，过B作BD⊥x轴于点D，

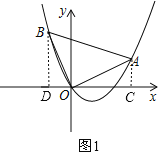
∵△AOB为等腰三角形，

∴AO=BO，

∵∠AOB=90°，

∴∠AOC+∠DOB=∠DOB+∠OBD=90°，

∴∠AOC=∠OBD，

在△ACO和△ODB中

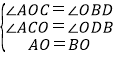
∴△ACO≌△ODB（AAS），

∵A（2，1），

∴OD=AC=1，BD=OC=2，

∴B（-1，2）；

（2）∵抛物线过O点，

∴可设抛物线解析式为y=ax2+bx，

把A、B两点坐标代入可得，解得，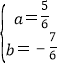

∴经过A、B、O原点的抛物线解析式为y=x2-x；

（3）∵四边形ABOP，

∴可知点P在线段OA的下方，

过P作PE∥y轴交AO于点E，如图2，

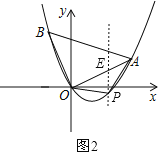
设直线AO解析式为y=kx，

∵A（2，1），

∴k=，

∴直线AO解析式为y=x，

设P点坐标为（t，t2-t），则E（t，t），

∴PE=t-（t2-t）=-t2+t=-（t-1）2+，

∴S△AOP=PE×2=PE═-（t-1）2+，

由A（2，1）可求得OA=OB=，

∴S△AOB=AOBO=，

∴S四边形ABOP=S△AOB+S△AOP=-（t-1）2++=，

∵-＜0，

∴当t=1时，四边形ABOP的面积最大，此时P点坐标为（1，-），

综上可知存在使四边形ABOP的面积最大的点P，其坐标为（1，-）．