题目内容
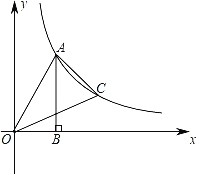
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
【答案】C
【解析】
根据二次函数图像的基本性质依次进行判断即可.
①当x=0时,y=m,∴点C的坐标为(0,m),该项正确;
②当m=0时,原函数解析式为:![]() ,此时对称轴为:
,此时对称轴为:![]() ,且A点交于原点,
,且A点交于原点,
∴B点坐标为:(2,0),即AB=2,∴D点坐标为:(1,1),根据勾股定理可得:BD=AD=![]() ,∴△ABD为等腰三角形,∵
,∴△ABD为等腰三角形,∵![]() ,∴△ABD为等腰直角三角形,该项正确;
,∴△ABD为等腰直角三角形,该项正确;
③由解析式得其对称轴为:![]() ,利用其图像对称性,∴当若a=-1,则b=3,该项错误;
,利用其图像对称性,∴当若a=-1,则b=3,该项错误;
④∵![]() +
+![]() >2,∴
>2,∴![]() ,又∵
,又∵![]() <1<
<1<![]() ,∴
,∴![]() -1<1<
-1<1<![]() -1,∴Q点离对称轴较远,∴
-1,∴Q点离对称轴较远,∴![]() >
>![]() ,该项正确;
,该项正确;
综上所述,①②④正确,③错误,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
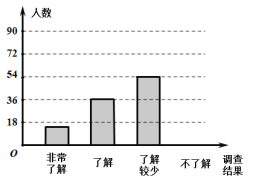
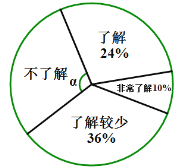
【题目】某中学抽取了40 名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数 /人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |

(1)求频数分布表中的m的值
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全统计图.
(3) 已知 该校有2000名学生,请你估计该校平均每周课外阅读时间在![]() 范围内的学生人数
范围内的学生人数