Question

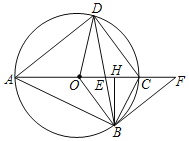
【题目】如图，点E在矩形ABCD对角线AC上由A向C运动，且BC＝2，∠ACB＝30°，连结EF，过点E作EF⊥DE，交BC于点F（当点F与点C重合时，点E也停止运动）

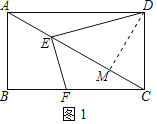
（1）如图1，当AC平分角∠DEF时，求AE的长度；

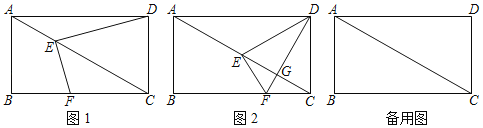
（2）如图2，连结DF，与AC交于点G，若DF⊥AC时，求四边形DEFC的面积；

（3）若点E分AC为1：2两部分时，求BF：FC．

Answer 1

【答案】（1）3﹣；（2）；（3）BF：CF＝4：5或BF：CF＝8：1．

【解析】

（1）如图1中，作DM⊥AC于M，解直角三角形求出CM，EM，AC即可解决问题；

（2）解直角三角形求出DG，FG，CG，利用相似三角形的性质求出EG，根据S四边形DEFC＝DFCE求解即可；

（3）分两种情形：①如图1﹣1中，若AE：CE＝1：2，作EM⊥BC于M，EN⊥CD于N．解直角三角形求出EN，DN，EM，再利用相似三角形的性质求出MF即可解决问题．②若AE：CF＝2：1时，同法可求．

解：（1）如图1中，作DM⊥AC于M，

∵四边形ABCD是矩形，

∴∠B＝∠BCD＝∠ADC＝90°，AB＝CD，AD＝BC＝，

∵∠ACB＝30°，

∴AB＝CD＝BCtan30°＝2，AC＝2AB＝4，

在Rt△CDM中，∵∠CMD＝90°，∠DCM＝60°，CD＝2，

∴∠CDM＝30°，

∴CM＝CD＝1，DM＝CM＝，

∵∠DEF＝90°，EM平分∠DEF，

∴∠DEM＝∠DEF＝45°，

∴EM＝DM＝，

∴AE＝AC﹣EM﹣CM＝3﹣；

（2）如图2中，

∵DF⊥AC，

∴∠DGC＝90°，

在Rt△CDG中，∵CD＝2，∠DCG＝60°，

∴∠CDG＝30°，

∴CG＝CD＝1，DG＝，

∴FG＝CGtan30°＝，

∵∠FEG+∠DEG＝90°，∠EDG+∠DEG＝90°，

∴∠FEG＝∠EDG，

∵∠EGF＝∠DGE＝90°，

∴△EGF∽△DGE，

∴，

∴，

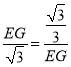∴EG＝1，

∴S四边形DEFC＝DFCE＝×2×＝；

（3）①如图1﹣1中，若AE：CE＝1：2，作EM⊥BC于M，EN⊥CD于N．

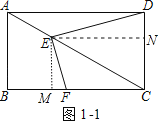
∵AB＝CD＝2，AC＝4，AE：EC＝1：2，

∴AE＝，EC＝，

在Rt△CEN中，∵∠ECN＝30°

∴CN＝EC＝，EN＝CN＝，

∴DN＝2﹣＝，

在Rt△CEM中，∵∠ECM＝30°，

∴EM＝EC＝，CM＝EM＝，

∵DE⊥EF，

∴∠DEF＝∠NEM＝90°，

∴∠DEN＝∠MEF，

∵∠END＝∠EMF＝90°，

∴△END∽△EMF，

∴ ，可得MF＝，

∴CF＝CM﹣MF＝，BF＝﹣CF＝，

∴BF：CF＝4：5；

②若AE：CF＝2：1时，同法可得BF：CF＝8：1．

综上所述，BF：CF＝4：5或BF：CF＝8：1．