Question

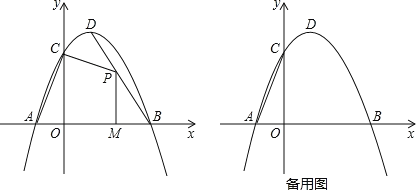
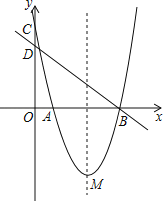
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与两坐标轴分别交于点A、B、C，直线y＝﹣x+4经过点B，与y轴交点为D，M（3，﹣4）是抛物线的顶点．

（1）求抛物线的解析式．

（2）已知点N在对称轴上，且AN+DN的值最小．求点N的坐标．

（3）在（2）的条件下，若点E与点C关于对称轴对称，请你画出△EMN并求它的面积．

（4）在（2）的条件下，在坐标平面内是否存在点P，使以A、B、N、P为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝x2﹣6x+5；（2）N(3，)；（3）画图见解析，S△EMN＝；（4）存在，满足条件的点P的坐标为（3，﹣）或（7，）或（﹣1，）．

【解析】

（1）先确定出点B坐标，最后用待定系数法即可得出结论；（2）先判断出点N是直线BC与对称轴的交点，即可得出结论；（3）先求出点E坐标，最后用三角形面积公式计算即可得出结论；（4）设出点P坐标，分三种情况利用用平行四边形的两条对角线互相平分和中点坐标公式求解即可得出结论．

解：（1）针对于直线y＝﹣x+4，

令y＝0，则0＝﹣x+4，

∴x＝5，

∴B（5，0），

∵M（3，﹣4）是抛物线的顶点，

∴设抛物线的解析式为y＝a（x﹣3）2﹣4，

∵点B（5，0）在抛物线上，

∴a（5﹣3）2﹣4＝0，

∴a＝1，

∴抛物线的解析式为y＝（x﹣3）2﹣4＝x2﹣6x+5；

（2）由（1）知，抛物线的解析式为y＝（x﹣3）2﹣4，

∴抛物线的对称轴为x＝3，

∵点A，B关于抛物线对称轴对称，

∴直线y＝﹣x+4与对称轴x＝3的交点就是满足条件的点N，

∴当x＝3时，y＝﹣×3+4＝，

∴N（3，）；

（3）∵点C是抛物线y＝x2﹣6x+5与y轴的交点，

∴C（0，5），

∵点E与点C关于对称轴x＝3对称，

∴E（6，5），

由（2）知，N（3，），

∵M（3，﹣4），

∴MN＝﹣（﹣4）＝，

∴S△EMN＝MN|xE﹣xM|＝××3＝；

（4）设P（m，n），

∵A（1，0），B（5，0），N（3，），

当AB为对角线时，AB与NP互相平分，

∴（1+5）＝（3+m），（0+0）＝（+n），

∴m＝3，n＝﹣，

∴P（3，﹣）；

当BN为对角线时，（1+m）＝（（3+5），（0+n）＝（0+），

∴m＝7，n＝，

∴P（7，）；

当AN为对角线时，（1+3）＝（5+m），（0+）＝（0+n），

∴m＝﹣1，n＝，

∴P（﹣1，），

即：满足条件的点P的坐标为（3，﹣）或（7，）或（﹣1，）．