题目内容
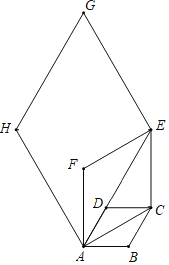
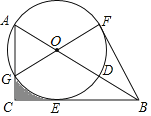
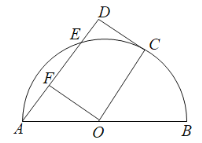
【题目】如图,已知![]() 是半圆的直径,圆心为
是半圆的直径,圆心为![]() 为半圆上的两个动点,且
为半圆上的两个动点,且![]() ,过点C作
,过点C作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() 于点F.
于点F.
(1)四边形![]() 的形状是______________________.
的形状是______________________.
(2)连接![]() ,若
,若![]() ,则当
,则当![]() 时四边形
时四边形![]() 为平行四边形;若四边形
为平行四边形;若四边形![]() 为菱形,四边形
为菱形,四边形![]() 的面积是
的面积是![]() ,求直径
,求直径![]() 的长.
的长.
【答案】(1)矩形;(2)k=1,![]()
【解析】
(1)依据“有三个角是直角的四边形是矩形”进行证明即可得到结论;
(2)先假设四边形AOCE为平行四边形,可证明四边形AOCE是菱形得AO=EC,再证明Rt△AOF≌Rt△ECD得DE=AF,从而可证DE=EF,进而可得结论;解Rt△EDC得![]() ,根据矩形OCDF的面积是
,根据矩形OCDF的面积是![]() 可求得
可求得![]() ,从而可得结论.
,从而可得结论.
(1)∵CD是![]() 的切线,
的切线,
∴OC⊥CD,∠OCD=90°,
∵![]()
∴F为AE的中点,∠OFE=90°,
∵![]()
∴∠OFE+∠COF=90°,
∠COF=90°
∴四边形![]() 是矩形.
是矩形.
故答案为:矩形
(2)假设四边形AOCE为平行四边形,
连接EC、EO, 如图,
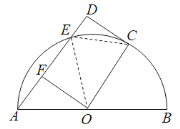
∵OA=OC,
四边形AOCE是菱形,
∵OE=OA,OF⊥AE,
∴AF=EF,
在Rt△AOF和Rt△ECD中,
![]()
∴Rt△AOF≌Rt△ECD,
∴DE=AF,
∴DE=EF,
∴![]() ,
,
即k=1时,四边形AOCE为平行四边形;
故答案为:1;
若四边形AOCE是菱形,则![]()
由于四边形OCDF是矩形,
所以在Rt△EDC中,![]()
∴由于矩形OCDF的面积是![]()
![]()
所以![]() 所以
所以![]()

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20