题目内容
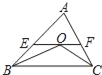
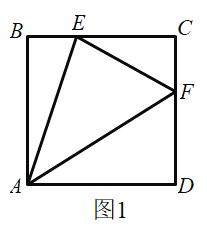
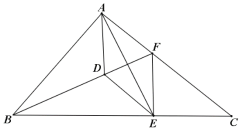
【题目】如图,点E,F分别在△ABC的边BC和AC上,点A,E关于BF对称.点D在BF上,且AD∥EF.
(1)求证:四边形ADEF为菱形;
(2)如果∠ABC=2∠DAE,AD=3,FC=5,求AB.
【答案】(1)见解析;(2)6
【解析】
(1)则题意知BF垂直平分AE,证得△ADF![]() △EDF,推出∠ADF=∠EDF结合AD//EF,推出∠EDF =∠DFE,从而得到AD=DE=EF=AF,即可推出结论;
△EDF,推出∠ADF=∠EDF结合AD//EF,推出∠EDF =∠DFE,从而得到AD=DE=EF=AF,即可推出结论;
(2)由(1)得四边形ADEF是菱形,推出AE⊥DF,结合已知根据“SSS”推出△BAF![]() △BEF,可证得∠FEC=90°,利用勾股定理得出EC的长,证得△CEF∽△CAB,即可求解.
△BEF,可证得∠FEC=90°,利用勾股定理得出EC的长,证得△CEF∽△CAB,即可求解.
(1)∵点A,E关于BF对称,
∴BF垂直平分AE,
∴AD=DE,AF=FE,
在△ADF和△EDF中,
 ,
,
∴△ADF![]() △EDF(SSS),
△EDF(SSS),
∴∠ADF=∠EDF,
∵AD//EF,
∴∠ADF=∠DFE,
∴∠EDF =∠DFE,
∴DE=EF,
∴AD=DE=EF=AF,
∴四边形ADEF是菱形;
(2)记AE、DF交点为点O,

∵四边形ADEF是菱形,
∴AE⊥DF,
∴∠AOB=90°,
∴∠EAF+∠AFB=90°,
由(1)知BF垂直平分AE,
∴BA=BE,
∴∠ABC=2∠ABO,
∵∠ABC=2∠DAE,
∴∠ABO=∠DAE,
∵四边形ADEF为菱形,
∴∠DAE=∠EAF,AD=DE=EF=AF=3,
∴∠ABO=∠EAF,
∴∠ABO+∠AFB=90°,
∴∠BAF=90°,
∵BA=BE,FA=EF,
在△BAF和△BEF中,
 ,
,
∴△BAF![]() △BEF (SSS),
△BEF (SSS),
∴∠BAF =∠BEF=90°,
∴∠FEC=90°,
在Rt△FEC中,∠FEC=90°,AD=EF=3,
∴EC=![]() ,
,
∵∠BAC=∠FEC=90°,
∴△CEF∽△CAB,
∴![]() ,
,
∴![]() ,
,
∴AB=6.