Question

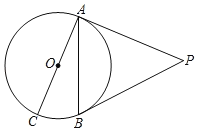
【题目】如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径．

（1）若∠BAC=25°，求∠P的度数；

（2）若∠P=60°，PA=2，求AC的长．

Answer 1

【答案】（1）50°；（2）4．

【解析】

（1）利用切线的性质求出∠PAB=90°﹣∠BAC=90°﹣25°=65°，根据切线长定理得到∠PBA=∠PAB=65°，再根据三角形的内角和定理求出∠P的度数；

（2）连接BC，证明△PAB是等边三角形，求出，∠PAB=60°，由AC是⊙O的直径得到∠ABC=90°，利用AC=求出答案.

（1）∵PA为切线，

∴OA⊥PA，

∴∠CAP=90°，

∴∠PAB=90°﹣∠BAC=90°﹣25°=65°．

∵PA，PB是⊙O的切线，

∴PA=PB，

∴∠PBA=∠PAB=65°，

∴∠P=180°﹣65°﹣65°=50°；

（2）连接BC．

∵PA，PB是⊙O的切线，

∴PA=PB，∠CAP=90°．

∵∠P=60°，

∴△PAB是等边三角形，

∴，∠PAB=60°，

∴∠CAB=30°．

∵AC是⊙O的直径，

∴∠ABC=90°，

∴AC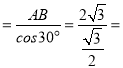4.