Question

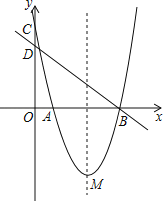
【题目】如图，已知抛物线y＝﹣x2+（m﹣1）x+m的对称轴为x＝，请你解答下列问题：

（1）m＝　 　，抛物线与x轴的交点为　 　．

（2）x取什么值时，y的值随x的增大而减小？

（3）x取什么值时，y＜0？

Answer 1

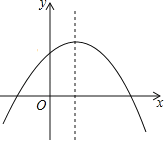
【答案】（1）2；（﹣1，0），（2，0）；（2）x＞；（3）x＜﹣1或x＞2

【解析】

（1）利用抛物线的对称轴方程得到=，解方程得到m的值，从而得到y＝x2＋x＋2，然后解方程x2＋x＋2＝0得抛物线与x轴的交点；（2）根据二次函数的性质求解；（3）结合函数图象，写出抛物线在x轴下方所对应的自变量的范围即可．

解：（1）抛物线的对称轴为直线x＝=，

∴m＝2，

抛物线解析式为y＝﹣x2+x+2，

当y＝0时，﹣x2+x+2＝0，解得x1＝﹣1，x2＝2，

∴抛物线与x轴的交点为（﹣1，0），（2，0）；

（2）由函数图象可知,

当x＞时，y的值随x的增大而减小；

（3）由函数图象可知,

当x＜﹣1或x＞2时，y＜0．