��Ŀ����
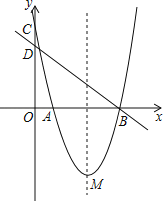
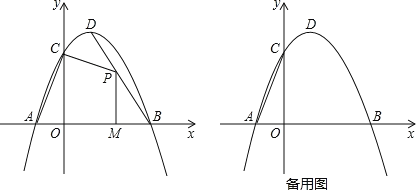
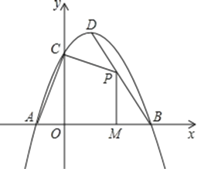
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��ax2+bx+3��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1����ֱ��AC�������ߵĽ���ʽ�������D������ꣻ
��2����PΪ�߶�BD�ϵ�һ�����㣬����P��PM��x���ڵ�M�����ı���PMAC����������ֵ�ʹ�ʱ��P�����ꣻ
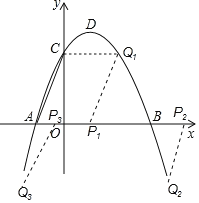
��3������P��x����һ�����㣬��P��ֱ��1��AC���������ڵ�Q����̽��������P����˶��������������Ƿ���ڵ�Q��ʹ�Ե�A��P��Q��CΪ������ı�����ƽ���ı��Σ������ڣ���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=3x+3��y=��x2+2x+3������D������Ϊ(1��4)����2���ı���PMAC����������ֵΪ![]() ����ʱ��P������Ϊ(
����ʱ��P������Ϊ(![]() ��
��![]() )����3����Q������Ϊ(2��3)��(1
)����3����Q������Ϊ(2��3)��(1![]() ����3)��(1
����3)��(1![]() ����3)��
����3)��
��������
��1���������C���꣬Ȼ�����ô���ϵ�����������ֱ��AC�������ߵĽ���ʽ���������ߵ�һ��ʽת��Ϊ����ʽ�������D������ꣻ
��2���ȸ��ݴ���ϵ�������ֱ��BD�Ľ���ʽ�����P�ĺ�����Ϊp��Ȼ�����S�ı���PMAC=S��OAC+S����OMPC���ɵó�S�ı���PMAC��p�Ĺ�ϵʽ���ٸ��ݶ��κ��������ʽ�ɣ�
��3���������PQ��AC��PQ=AC�����P������Ϊ(x��0)������Q��x���Ϸ�ʱ�����Q������Ϊ(x+1��3)���ѵ�Q��������������ߵĽ���ʽ�������x�������ɵõ�Q���ꣻ����Q��x���·�ʱ�����Q������Ϊ(x��1����3)��ͬ���ķ�����⼴�ɣ�
��1����������y=��ax2+bx+3��y�ύ�ڵ�C��
���C(0��3)��
��ֱ��AC�Ľ���ʽΪy=k1x+b1(k1��0)��
�ߵ�A(��1��0)����C(0��3)��
��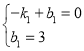 ����ã�
����ã�![]() ��
��
��ֱ��AC�Ľ���ʽΪy=3x+3��
��������y=��ax2+bx+3��x�ύ��A(��1��0)��B(3��0)���㣬
��![]() ����ã�
����ã�![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��y=��x2+2x+3=��(x��1)2+4��
�ඥ��D������Ϊ(1��4)��
��2����ֱ��BD�Ľ���ʽΪy=kx+b��
�ߵ�B(3��0)����D(1��4)��
��![]() ����
����![]() ��
��
��ֱ��BD�Ľ���ʽΪy=��2x+6��
��PΪ�߶�BD�ϵ�һ�����㣬
�����P������Ϊ(p����2p+6)��
��OA=1��OC=3��OM=p��PM=��2p+6��
��S�ı���PMAC=S��OAC+S����OMPC![]() =��p2
=��p2![]() p
p![]() =��(p
=��(p![]() )2
)2![]() ��
��
��1��p��3��
�൱p![]() ʱ���ı���PMAC�����ȡ�����ֵΪ
ʱ���ı���PMAC�����ȡ�����ֵΪ![]() ����ʱ��P������Ϊ(
����ʱ��P������Ϊ(![]() ��
��![]() )��
)��
��3����ֱ��l��AC���Ե�A��P��Q��CΪ������ı�����ƽ���ı��Σ�
��PQ��AC��PQ=AC��
���P������Ϊ(x��0)����A(��1��0)��C(0��3)��
����Q��x���Ϸ�ʱ�����Q������Ϊ(x+1��3)��
��ʱ����(x+1)2+2(x+1)+3=3��
��ã�x1=��1(��ȥ)��x2=1��
���Q������Ϊ(2��3)��
����Q��x���·�ʱ�����Q������Ϊ(x��1����3)��
��ʱ����(x��1)2+2(x��1)+3=��3��
�����ã�x2��4x��3=0��
��ã�x1=2![]() ��x2=2
��x2=2![]() ��
��
���Q������Ϊ(1![]() ����3)��(1
����3)��(1![]() ����3)��
����3)��
������������Q������Ϊ(2��3)��(1![]() ����3)��(1
����3)��(1![]() ����3)��
����3)��

 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�����Ŀ��Ϊ�˰�������һ��������Ѫ�����ĸ�������ij��15��ͬѧ���������Ǿ���������±���
���������λ��Ԫ�� | 5 | 10 | 20 | 50 | 100 |
������������� | 2 | 4 | 5 | 3 | 1 |
������15��ͬѧ�������������˵����ȷ����
A.������100 B.ƽ������30 C.������20 D.��λ����20