题目内容
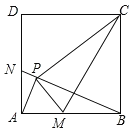
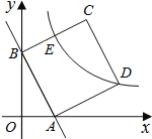
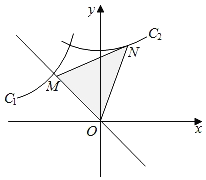
【题目】已知反比例函数C1:y=﹣![]() (x<0)的图象如图所示,将该曲线绕原点O顺时针旋转45°得到曲线C2,点N是曲线C2上的一点,点M在直线y=﹣x上,连接MN,ON,若MN=ON,则△MON的面积为_____.
(x<0)的图象如图所示,将该曲线绕原点O顺时针旋转45°得到曲线C2,点N是曲线C2上的一点,点M在直线y=﹣x上,连接MN,ON,若MN=ON,则△MON的面积为_____.
【答案】5.
【解析】
将直线y=﹣x和曲线C2绕点O逆时针旋转45°,则直线y=﹣x与x轴重合,曲线C2与曲线C1重合,再根据反比例函数K的几何意义即可求解.
解:若将直线y=﹣x和曲线C2绕点O逆时针旋转45°,
则直线y=﹣x与x轴重合,曲线C2与曲线C1重合,
∴旋转后点N落在曲线C1上,点M落在x轴上,如图所示,
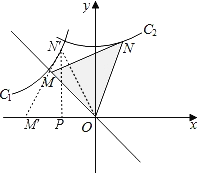
设点M,N的对应点分别是M',N',
过点N'作N'P⊥x轴于点P,连接ON',M'N'.
∵MN=ON,
∴M'N'=ON',M'P=PO,
∴S△MON=S△M′ON′=2S△ON′P=2×![]() =5;
=5;
故答案为:5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目