Question

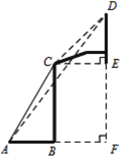
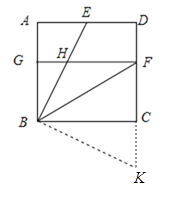
【题目】在边长为2的正方形ABCD中，点E是AD边上的中点，BF平分∠EBC交CD于点F，过点F作FG⊥AB交BE于点H，则GH的长为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

将△ABE绕B点旋转，使AB和BC重合，设△BCK是旋转后的△ABE，证明BE＝AE+CF，由勾股定理得BE＝，则CF＝BE﹣AE＝﹣1，易证四边形BCFG与四边形ADFG都是矩形，得出CF＝BG＝﹣1，GH∥AE，则△BGH∽△BAE，得出，即可得出结果．

解：∵四边形ABCD是正方形，

∴AB＝BC，∠BAE＝∠BCD＝90°，

将△ABE绕B点旋转，使AB和BC重合，如图所示：

设△BCK是旋转后的△ABE，

∴△ABE≌△CBK，

∴AE＝CK，BE＝BK，∠ABE＝∠CBK，∠BAE＝∠BCK＝90°，

∴K、C、F三点共线，

∵BF是∠EBC的角平分线，

∴∠EBF＝∠FBC，

∴∠ABE+∠EBF＝∠KBC+∠FBC，

∴∠ABF＝∠FBK，

∵四边形ABCD是正方形，

∴AB＝AD＝2，AB∥CD，

∴∠ABF＝∠BFK，

∴∠KBF＝∠BFK，

∴BK＝KF，

∵KF＝CK+CF＝AE+CF，BK＝BE，

∴BE＝AE+CF，

∵点E是AD边上的中点，

∴AE＝AD＝1，

由勾股定理得：BE＝，

∴CF＝BE﹣AE＝﹣1，

∵四边形ABCD是正方形，FG⊥AB，

∴四边形BCFG与四边形ADFG都是矩形，

∴CF＝BG＝﹣1，GH∥AE，

∴△BGH∽△BAE，

∴，即，

∴GH＝，

故选：A．