题目内容
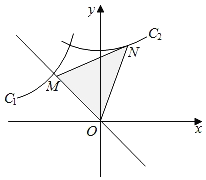
【题目】如图，直线AB：y=kx+b与x轴．y轴分别相交于点A（1，0）和点B（0，2），以线段AB为边在第一象限作正方形ABCD．
（1）求直线AB的解析式；
（2）求点D的坐标；
（3）若双曲线
（k＞0）与正方形的边CD绐终有一个交点，求k的取值范围．
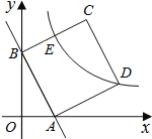
【答案】（1）y=-2x+2；（2）点D的坐标为（3，1）；（3）3≤k≤6．
【解析】
（1）根据点A，B的坐标，利用待定系数法可求出直线AB的解析式；
（2）作DF⊥x轴于F，易证△ADF≌△BAO（AAS），利用全等三角形的性质可求出点D的坐标；
（3）同（2）可求出点C的坐标，利用极限值法可求出k的最大．最小值，此题得解．
解：（1）将A（1，0），B（0，2）代入y=kx+b，得：
，解得：
，
∴直线AB的解析式为y=-2x+2．
（2）作DF⊥x轴于F，则∠AFD=90°，
∵正方形ABCD，
∴BA=AD，∠BAD=90°，∠BAO+∠DAF=90°，
∵∠BAO+∠ABO=90°，
∴∠ABO=∠DAF．
在△ADF和△BAO中，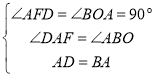
，
∴△ADF≌△BAO（AAS），
∴AF=BO=2，DF=AO=1，OF=OA+AF=3，
∴点D的坐标为（3，1）．
（3）同（2）可得出点C的坐标为（2，3）．
当双曲线过点D时，k=3×1=3；
当双曲线过点C时，k=2×3=6，
∴当双曲线
（k＞0）与正方形的边CD绐终有一个交点时，k的取值范围为3≤k≤6．
练习册系列答案
阅读快车系列答案
相关题目
