Question

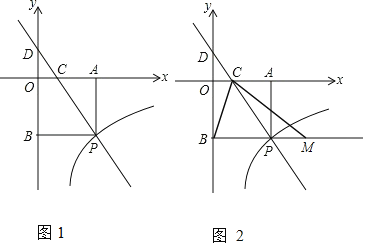
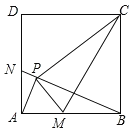
【题目】已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM，延长BP交AD于点N，连结CM．分析下列结论：①AP⊥BN；②BM＝DN；③点P一定在以CM为直径的圆上；④正方形内不存在点P使得PC＝．其中结论正确的个数是（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

由△PBC∽△PAM，得出∠PAM＝∠PBC，＝＝，即可推出AP⊥BN，故①正确；易证△BAP∽△BNA，得出＝，则＝，得出AM＝AN，即可得出BM＝DN，故②正确；由△PBC∽△PAM，得出∠APM＝∠BPC，推出∠CPM＝∠APB＝90°，即可得出点P一定在以CM为直径的圆上，故③正确；以点C为圆心为半径画圆，以AB为直径画圆，得出两个圆相切，则∠APB＝90°，即AP⊥PB，得出正方形内存在点P使得PC＝，故④错误；即可得出结果．

解：∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，∠DAB＝∠ABC＝∠BCD＝∠D＝90°，

∵△PBC∽△PAM，

∴∠PAM＝∠PBC，＝＝，

∵∠PBC+∠PBA＝90°，

∴∠PAM+∠PBA＝90°，

∴∠APB＝90°，

∴AP⊥BN，故①正确；

∵∠ABP＝∠ABN，∠APB＝∠BAN＝90°，

∴△BAP∽△BNA，

∴＝，

∴＝,

∵AB＝BC，

∴AM＝AN，

∴AB﹣AM＝AD﹣AN，

∴BM＝DN，故②正确；

∵△PBC∽△PAM，

∴∠APM＝∠BPC，

∴∠CPM＝∠APB＝90°，

∴点P一定在以CM为直径的圆上，故③正确；

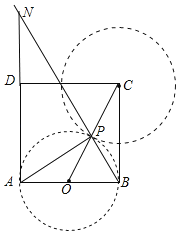
以点C为圆心为半径画圆，以AB为直径画圆，如图所示：

∴CO＝＝，

∵+＝，

∴两个圆相切，

∴∠APB＝90°，即AP⊥PB，

∵∠PBC＝∠PAB，

∴只要作∠APM＝∠BPC，就可得出△PBC∽△PAM，符合题意，

∴正方形内存在点P使得PC＝，故④错误；

综上所述，结论正确的个数是3，

故选：C．