��Ŀ����
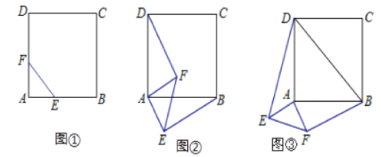
����Ŀ����1����ͼ�٣�������ABCD����E����F�ֱ���AB��AD�ϣ���AE=AF����ʱ���߶�BE��DF��������ϵ�� ��λ�ù�ϵ�� ����ֱ��д�����ۣ�
(2)��ͼ��,����ֱ��������FAE��ֱ�Ƕ���A˳ʱ����ת�Ϧ�,��0��<��<90��ʱ,����BE��DF,��ʱ(1)�еĽ����Ƿ�����������������֤�����������������˵�����ɡ�
(3)��ͼ��,����ֱ��������FAE��ֱ�Ƕ���A˳ʱ����ת�Ϧ�,��90��<��<180��ʱ������BD��DE��EF��FB���õ��ı���BDEF����˳�������ı���BDEF�����е�����ɵ��ı�����ʲô�����ı���?��ֱ��д������.
���𰸡���1��BE=DF��BE��DF����2��BE=DF��BE��DF��֤������������3��������.
��������
��1�����������ε����ʿɵ�AB=AD����A=90����Ȼ�����BE=DF��BE��DF��
��2��������ת�������BAE=��DAF��Ȼ���������߽DZ���֤����ABE����ADFȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�BE=DF��ȫ�������ζ�Ӧ����ȿɵá�ABE=��ADF���ӳ�DF��BE��O�������ABE+��2=90�����Ӷ��õ���BOD=90�������ݴ�ֱ�Ķ���õ�BE��DF��
��3������BE��DF��ͬ�����BE=DF��BE��DF���ٸ��ݶԽ�������һ��ഹֱ���ı��ε��е���ɵ��ı����������ν��
(1)��������ABCD��AB=AD����A=90����
��AE=AF��
��ABAE=ADAF��
��BE=DF��
�ߡ�A=90����
��BE��DF��
��BE=DF��BE��DF��
(2)�ߡ�FAE�ǵ���ֱ�������Σ�
��AE=AF��
��������ABCD��AB=AD��
�֡ߡ�BAE=��DAF=����
������ABE����ADF��
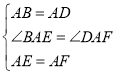 ��
��
���ABE�ա�ADF(SAS)��
��BE=DF����ABE=��ADF��
�ӳ�DF��BE��O��
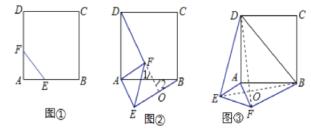
�ߡ�ADF+��1=90������1=��2(�Զ������)��
���ABE+��2=90����
���BOD=180��90��=90����
��BE��DF��
��BE=DF��BE��DF��
(3)����BE��DF��
��(2)ͬ�����BE=DF��BE��DF��
��˳�������ı���BDEF�����е�����ɵ��ı�����������.

 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�����Ŀ��ѧУͨ�������������Ӽס��ҡ������������Ƽ�һ����Ϊ�ؼ��Ƚ��༯�壬�±�����������������ʿ����÷ֱ���
�������ʿ����÷ֱ�����λ���֣�
�༶ | ��Ϊ�淶 | ѧϰ�ɼ� | У�˶��� | ������ | �Ͷ����� |
�װ� | 10 | 10 | 6 | 10 | 7 |
�Ұ� | 10 | 8 | 8 | 9 | 8 |
���� | 9 | 10 | 9 | 6 | 9 |
����ͳ�Ʊ��е���Ϣ�ش��������⣺
��1�����㲹ȫ����ɼ������������е����ݣ�
�༶ | ƽ���� | ���� | ��λ�� |
�װ� | 8.6 | 10 | �� |
�Ұ� | 8.6 | �� | 8 |
���� | �� | 9 | 9 |
��2�������ϱ��е����ݣ����Ƽ��ĸ���Ϊ�ؼ��Ƚ��༯�壿��˵�����ɡ�
��3�����ѧУ����Ϊ�淶��ѧϰ�ɼ���У�˶��ᡢ�������Ͷ�����������ɼ�����3��2��1��1��3�ı�ȷ���༶���ۺϳɼ���ѧ����������ʦ��������ۺϳɼ���������һ��������������ͳ��ͼ���뽫���ͳ��ͼ������������������ɼ���Ӧ�Ƽ��ĸ���Ϊ�ؼ��Ƚ��༯�壿Ϊʲô��