题目内容
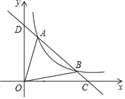
【题目】如图,已知直线y=kx+b与反比例函数y=![]() 的图象交于A(1,m)、B两点,与x 轴、y轴分别相交于C(4,0)、D两点.
的图象交于A(1,m)、B两点,与x 轴、y轴分别相交于C(4,0)、D两点.
(1)求直线y=kx+b的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)直接写出关于x的不等式kx+b<![]() 的解集是 .
的解集是 .
【答案】(1)y=﹣x+4;(2)4;(3)0<x<1或x>3.
【解析】分析:
(1)由已知条件易得点A的坐标,再将点A和C的坐标代入一次函数的解析式列出方程组,解得k和b的值即可得到一次函数的解析式;
(2)把两个函数的解析式组成方程组,解方程组即可求得点A和B的坐标,结合点C的坐标即可由S△AOB=S△AOC-S△BOC求得所求面积了;
(3)结合(2)中所得点A和点B的坐标和图象即可求得该不等式的解集了.
详解:
(1)将A(1,m)代入y=![]() ,得m=3,
,得m=3,
∴A(1,3),
将A(1,3)和C(4,0)分别代入y+kx+b,得:
![]() ,
,
解得:k=﹣1,b=4,
∴直线解析式为:y=﹣x+4.
(2)联立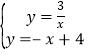 ,解得
,解得![]() 或
或 ![]() ,
,
∵点A的坐标为(1,3),
∴点B的坐标为(3,1),
∴S△AOB=S△AOC﹣S△BOC
=![]() OC|yA|﹣
OC|yA|﹣![]() OC|yB|
OC|yB|
=![]() ×4×3﹣
×4×3﹣![]() ×4×1
×4×1
=4
∴△AOB的面积为4.
(3)∵点A和B的坐标分别为A(1,3)和(3,1),
∴观察图象可知:不等式kx+b<![]() 的解集是0<x<1或x>3.
的解集是0<x<1或x>3.
故答案为0<x<1或x>3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目