题目内容
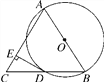
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
【答案】(1)证明见解析(2)2![]()
【解析】【试题分析】(1)连接AD.利用中垂线的性质证明即可;(2)∵∠BAC=60°,由(1)知AB=AC,根据有一角是60°的等腰三角形是等边三角形,得:△ABC是等边三角形,根据等边三角形的性质得:∠C=60°.因为AB=2×4=8,则DC=![]() BC=
BC=![]() AB=4.又∵因为DE⊥AC,根据三角形函数解得:DE=DC·sinC=4·sin60°=2
AB=4.又∵因为DE⊥AC,根据三角形函数解得:DE=DC·sinC=4·sin60°=2![]() .
.
【试题解析】
(1)连接AD.∵AB是⊙O的直径,∴∠ADB=90°.∵DC=BD,∴AB=AC.
(2)∵∠BAC=60°,由(1)知AB=AC,∴△ABC是等边三角形,∴∠C=60°.
∵AB=2×4=8,∴DC=![]() BC=
BC=![]() AB=4.又∵DE⊥AC,∴DE=DC·sinC=4·sin60°=2
AB=4.又∵DE⊥AC,∴DE=DC·sinC=4·sin60°=2![]() .
.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目