题目内容
【题目】设k≠0,若函数y1=kx+3,y2=(x﹣k)2+k和y3=(x+k)2﹣k的图象与y轴依次交于A,B和C三点,设函数y2,y3的图象的顶点分别为D,E.
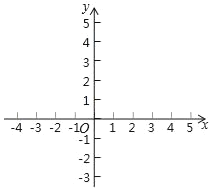
(1)当k=1时,请在直角坐标系中,分别画出函数y1,y2,y3的草图,并根据图象,写出你发现的两条结论;
(2)BC长与k之间是正比例函数关系吗?请作出判断,并说明理由;
(3)若△ADE的面积等于9,求y2随x的增大而减小时,x的取值范围.
【答案】(1)见解析,直线与两抛物线始终有两个交点;B点在C点上方;(2)BC长与k之间是正比例函数关系,见解析;(3)x≤3.
【解析】
(1)当k=1时,分别求出它们的解析式,画出图象;
(2)求出B与C的坐标,求出BC=2k,可知BC与k是正比例函数;
(3)构造矩形求△BDE的面积,利用面积求k的值,进而求出y2的函数解析式,从而求解.
解:(1)当k=1时,y1=x+3,y2=(x﹣1)2+1和y3=(x+1)2﹣1.
如图,
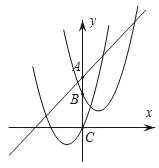
直线与两抛物线始终有两个交点;B点在C点上方;
(2)B(0,k2+k),C(0,k2﹣k),
∴BC=(k2+k)﹣(k2﹣k)=2k,
∴BC长与k之间是正比例函数关系;
(3)由表达式可知:D(k,k),E(﹣k,﹣k),
过D,E分别向x轴作垂线,过A,E分别向y轴作垂线,交点为O,P,E,N,
则由OPEN构造长方形,
∴S△ADE=SPONE﹣S△APE﹣S△AOD﹣S△EDN=2k(3+k)﹣![]() k(3+k)﹣
k(3+k)﹣![]() 2k2k﹣
2k2k﹣![]() k(3﹣k)=3k,
k(3﹣k)=3k,
∵△ADE的面积等于9,
∴3k=9,
∴k=3,
∴y2=(x﹣k)2+k=(x﹣3)2+3,
∴对称轴是x=3,
当y2随x的增大而减小时,x≤3.
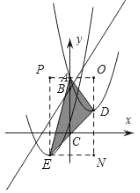
故答案为:(1)见解析,直线与两抛物线始终有两个交点;B点在C点上方;(2)BC长与k之间是正比例函数关系,见解析;(3)x≤3.

 阅读快车系列答案
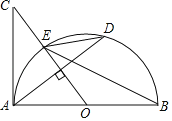
阅读快车系列答案【题目】如图,在半圆弧![]() 中,直径
中,直径![]() cm,点
cm,点![]() 是
是![]() 上一点,
上一点,![]() cm,
cm,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() ,设
,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm,
cm,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm,
cm,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm.小东根据学习函数的经验,分别对函数
cm.小东根据学习函数的经验,分别对函数![]() 、
、![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究:
的变化而变化的规律进行了探究:

下面是小东的探究过程,请补充完整:
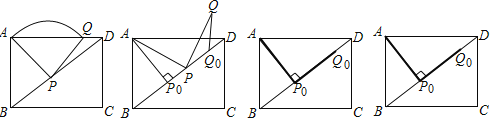
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值;
的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点(
中,描出补全后的表中各组数值所对应的点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象;
的图象;
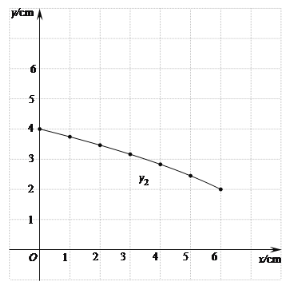
(3)结合函数图象,解决问题:①当![]() 时,线段
时,线段![]() 的取值范围是 ;②当
的取值范围是 ;②当![]() 是等腰三角形时,线段AP的长约为 .
是等腰三角形时,线段AP的长约为 .