题目内容
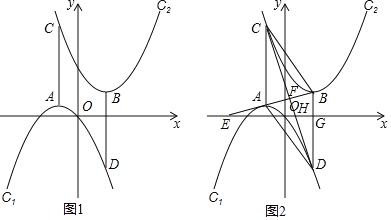
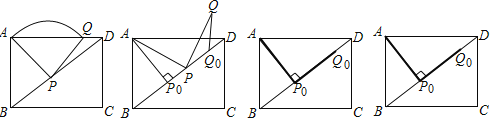
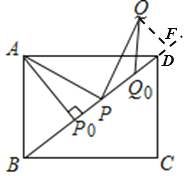
【题目】如图,在矩形ABCD中,AB=3,AD=4,P沿射线BD运动,连接AP,将线段AP绕点P顺时针旋转90°得线段PQ.
(1)当点Q落到AD上时,∠PAB=____°,PA=_____,![]() 长为_____;
长为_____;
(2)当AP⊥BD时,记此时点P为P0,点Q为Q0,移动点P的位置,求∠QQ0D的大小;
(3)在点P运动中,当以点Q为圆心,![]() BP为半径的圆与直线BD相切时,求BP的长度;
BP为半径的圆与直线BD相切时,求BP的长度;
(4)点P在线段BD上,由B向D运动过程(包含B、D两点)中,求CQ的取值范围,直接写出结果.
【答案】(1)45,![]() ,
,![]() π;(2)满足条件的∠QQ0D为45°或135°;(3)BP的长为
π;(2)满足条件的∠QQ0D为45°或135°;(3)BP的长为![]() 或
或![]() ;(4)
;(4)![]() ≤CQ≤7.
≤CQ≤7.
【解析】
(1)由已知,可知△APQ为等腰直角三角形,可得∠PAB,再利用三角形相似可得PA,及弧AQ的长度;
(2)分点Q在BD上方和下方的情况讨论求解即可.
(3)分别讨论点Q在BD上方和下方的情况,利用切线性质,在由(2)用BP0表示BP,由射影定理计算即可;
(4)由(2)可知,点Q在过点Qo,且与BD夹角为45°的线段EF上运动,有图形可知,当点Q运动到点E时,CQ最长为7,再由垂线段最短,应用面积法求CQ最小值.
解:(1)如图,过点P做PE⊥AD于点E
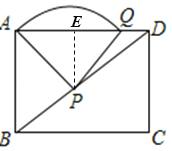
由已知,AP=PQ,∠APQ=90°
∴△APQ为等腰直角三角形
∴∠PAQ=∠PAB=45°
设PE=x,则AE=x,DE=4﹣x
∵PE∥AB
∴△DEP∽△DAB
∴![]() =
=![]()
∴![]() =
=![]()
解得x=![]()
∴PA=![]() PE=
PE=![]()
∴弧AQ的长为![]() 2π
2π![]() =
=![]() π.
π.
故答案为:45,![]() ,
,![]() π.
π.
(2)如图,过点Q做QF⊥BD于点F
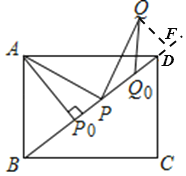
由∠APQ=90°,
∴∠APP0+∠QPD=90°
∵∠P0AP+∠APP0=90°
∴∠QPD=∠P0AP
∵AP=PQ
∴△APP0≌△PQF
∴AP0=PF,P0P=QF
∵AP0=P0Q0
∴Q0D=P0P
∴QF=FQ0
∴∠QQ0D=45°.
当点Q在BD的右下方时,同理可得∠PQ0Q=45°,
此时∠QQ0D=135°,
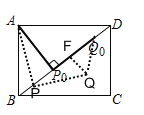
综上所述,满足条件的∠QQ0D为45°或135°.
(3)如图当点Q直线BD上方,当以点Q为圆心,![]() BP为半径的圆与直线BD相切时
BP为半径的圆与直线BD相切时
过点Q做QF⊥BD于点F,则QF=![]() BP
BP
由(2)可知,PP0=![]() BP
BP
∴BP0=![]() BP
BP
∵AB=3,AD=4
∴BD=5
∵△ABP0∽△DBA
∴AB2=BP0BD
∴9=![]() BP×5
BP×5
∴BP=![]()
同理,当点Q位于BD下方时,可求得BP=![]()
故BP的长为![]() 或
或![]()
(4)由(2)可知∠QQ0D=45°
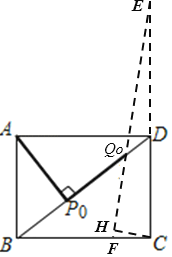
则如图,点Q在过点Q0,且与BD夹角为45°的线段EF上运动,
当点P与点B重合时,点Q与点F重合,此时,CF=4﹣3=1
当点P与点D重合时,点Q与点E重合,此时,CE=4+3=7
∴EF=![]() =
=![]() =5
=5![]()
过点C做CH⊥EF于点H
由面积法可知
CH=![]() =
=![]() =
=![]()
∴CQ的取值范围为:![]() ≤CQ≤7
≤CQ≤7