题目内容
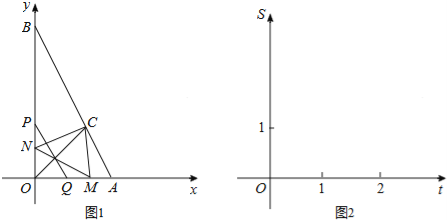
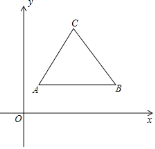
【题目】如图,在平面直角坐标系的第一象限中,有一点A(1,2),AB∥x轴且AB=6,点C在线段AB的垂直平分线上,且AC=5,将抛物线y=ax2(a>0)的对称轴右侧的图象记作G.
(1)若G经过C点,求抛物线的解析式;
(2)若G与△ABC有交点.
①求a的取值范围;②当0<y≤8时,双曲线![]() 经过G上一点,求k的最大值.
经过G上一点,求k的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②k的最大值为112.
,②k的最大值为112.
【解析】
(1)如图1中,作CH⊥AB于H.求出点C坐标即可解决问题;
(2)①当抛物线经过点A时,a=2,当抛物线经过点B时,2=49a,可得a=![]() ,由此即可解决问题;
,由此即可解决问题;
②由题意当a=![]() 时,y=
时,y=![]() x2,当y=8时,8=
x2,当y=8时,8=![]() x2,因为x>0,推出x=14,由题意当反比例函数y=
x2,因为x>0,推出x=14,由题意当反比例函数y=![]() 经过点(14,8)时k的值最大;
经过点(14,8)时k的值最大;
解:(1)如图1中,作CH⊥AB于H.
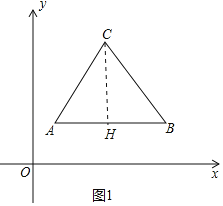
∵CA=CB=5,CH⊥AB,
∴AH=HB=3,
在Rt△ACH中,CH=![]() =4,
=4,
∴C(4,6),
∵抛物线y=ax2(a>0)经过C点,
∴6=16a,
∴a=![]() ,
,
∴抛物线的解析式为y=![]() x2.
x2.
(2)①∵A(1,2),B(7,2),
当抛物线经过点A时,a=2,
当抛物线经过点B时,2=49a,
∴a=![]() ,
,
∵若G与△ABC有交点,
∴![]() ≤a≤2.
≤a≤2.
②由题意当a=![]() 时,y=
时,y=![]() x2,
x2,
当y=8时,8=![]() x2,
x2,
∴x>0,
∴x=14,
∴当反比例函数y=![]() 经过点(14,8)时k的值最大,此时k=112,
经过点(14,8)时k的值最大,此时k=112,
∴k的最大值为112.

练习册系列答案
相关题目