题目内容
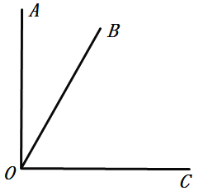
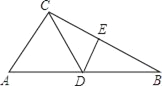
【题目】如图，Rt△OAB的顶点O与坐标原点重合，∠AOB=90°，AO=2BO，当点A在反比例函数
（x＞0）的图像上移动时，点B的坐标满足的函数表达式为（ ）
A. 
（x＜0） B. 
（x＜0）
C. 
（x＜0） D. 
（x＜0）
【答案】B
【解析】过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设B点坐标满足的函数解析式是y=
，易得△AOC∽△OBD，然后由相似三角形面积比等于相似比的平方，求得S△AOC：S△BOD=4，继而求得答案．
如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设B点坐标满足的函数解析式是y=，∴∠ACO=∠BDO=90°，∴∠AOC+∠OAC=90°．
∵∠AOB=90°，∴∠AOC+∠BOD=90°，∴∠BOD=∠OAC，∴△AOC∽△OBD，∴S△AOC：S△BOD=（
）2．
∵AO=2BO，∴S△AOC：S△BOD=4．
∵当A点在反比例函数y=
（x＞0）的图象上移动，∴S△AOC=
OCAC=x=1，∴S△BOD=DOBD=（﹣x）=﹣k，∴1=4×（﹣k），解得：k=﹣
∴B点坐标满足的函数解析式y=﹣
（x＜0）．
故选B．
练习册系列答案
优生乐园系列答案
相关题目
