题目内容
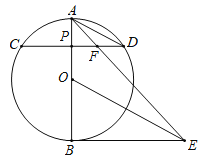
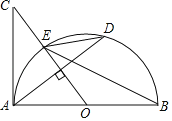
【题目】如图,AB是半圆O的直径,D为半圆上的一个动点(不与点A,B重合),连接AD,过点O作AD的垂线,交半圆O的切线AC于点C,交半圆O于点E.连接BE,DE.
(1)求证:∠BED=∠C.
(2)连接BD,OD,CD.
填空:
①当∠ACO的度数为 时,四边形OBDE为菱形;
②当∠ACO的度数为 时,四边形AODC为正方形.
【答案】(1)证明见解析;(2)①30°;②45°.
【解析】
(1)利用同角的余角相等证明∠BED=∠C;
(2)①当∠ACO=30°时,四边形OBDE是菱形,利用邻边相等的平行四边形为菱形进行证明;
②当∠ACO=45°时,四边形AODC是正方形,利用利用邻边相等的矩形为正方形进行证明.
(1)r如图,设AD,OC交于点P,
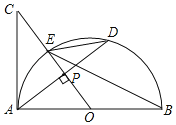
∵OC⊥AD,
∴∠APC=90°.
∴∠C+∠CAP=180°﹣∠APC=90°
∵AC是半圆O的切线,
∴∠CAO=∠CAP+∠BAD=90°.
∴∠BAD=∠C,
∵∠BED=∠BAD,
∴∠BED=∠C;
(2)①当∠ACO=30°时,四边形OBDE是菱形,理由如下
连接BD,如图

∵AB是半圆O的直径,
∴∠ADB=90°,
∵∠DAB=∠ACO=30°,
∴∠DBA=60°,
∵OE⊥AD,
∴![]() =
=![]()
∴∠DBE=∠ABE=30°
∵∠DEB=∠DAB=30°,
∴∠DEB=∠ABE,
DE∥AB
∵∠ADB=90°,即BD⊥AD,
OE⊥AD,
∴OE∥BD,
故四边形OBDE 是平行四边形
∵OB=OE
∴四边形OBDE 是菱形;
故答案为30°;
②当∠ACO=45°时,四边形AODC是正方形.理由如下
连接CD、OD,
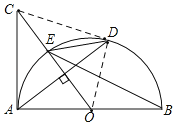
∵∠BED=∠ACO=45°,
∴∠BOD=2∠BED=90°,
∴∠AOD=90°,
∵OC⊥AD,
∴OC垂直平分AD
∴∠OCD=∠OCA=45°,
∴∠ACD=90°,
∵∠ACO=90°,
∴四边形AODC是矩形
∵OA=OD,
∴四边形AODC是正方形,
故答案为45°.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案