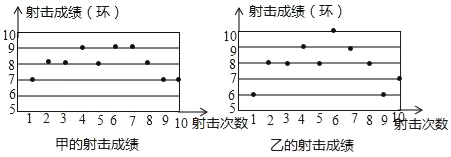
��Ŀ����
����Ŀ��ij�Ƽ���˾�ӵ�һ�����߿Ƽ���Ʒ����������Ҫ����![]() ���ڣ���
���ڣ���![]() �죩�������Ϊ�������Ч�ʣ������Ӱ�ӵ㣬�ӵ�����ĵ�һ��������˸��ֲ�Ʒ
�죩�������Ϊ�������Ч�ʣ������Ӱ�ӵ㣬�ӵ�����ĵ�һ��������˸��ֲ�Ʒ![]() �����Ժ�ÿ�������IJ�Ʒ����ǰһ���
�����Ժ�ÿ�������IJ�Ʒ����ǰһ���![]() �������ڻ�����ĵ�ԭ���������IJ�Ʒ�����ﵽ
�������ڻ�����ĵ�ԭ���������IJ�Ʒ�����ﵽ![]() ����ÿ������һ�����������������в�Ʒƽ��ÿ���ɱ�������
����ÿ������һ�����������������в�Ʒƽ��ÿ���ɱ�������![]() Ԫ��
Ԫ��
��1�����![]() ��������Ʒ
��������Ʒ![]() �������
�������![]() ��
��![]() ֮��ĺ�������ʽ����д���Ա���
֮��ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����ò�Ʒÿ�������ɱ�����������������![]() ��ʱ��Ϊ
��ʱ��Ϊ![]() Ԫ�������۸�Ϊÿ��
Ԫ�������۸�Ϊÿ��![]() Ԫ�����
Ԫ�����![]() �������Ϊ
�������Ϊ![]() Ԫ������
Ԫ������![]() ��
��![]() ֮��ĺ�������ʽ������ù�˾��һ���õ�����������������Ƕ��٣�
֮��ĺ�������ʽ������ù�˾��һ���õ�����������������Ƕ��٣�
��3���ù�˾�����������![]() Ԫ�����ļ��죿��ֱ��д�������
Ԫ�����ļ��죿��ֱ��д�������
���𰸡���1��![]() ��xΪ������������2��
��x������������2��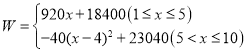 ����
����![]() ����������������Ϊ
����������������Ϊ![]() Ԫ����3��������
Ԫ����3��������![]() Ԫ���ǵ�5��6��7��
Ԫ���ǵ�5��6��7��
��������
��1���ɵ�һ��������![]() �����Ժ�ÿ�춼��ǰһ�������
�����Ժ�ÿ�춼��ǰһ�������![]() �����ɵó�
�����ɵó�![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2�����ղ���������50���ղ�������50��������������ۣ���������ʽ�г�������ϵʽ�����ú��������ʼ��䷽��ȡ������������ֵ���ɣ�
��3�����������г�����ʽ������⣬Ȼ��ȡ�������ɣ�
�⣺��1���ߵ�һ��������![]() �����Ժ�ÿ�춼��ǰһ�������
�����Ժ�ÿ�춼��ǰһ�������![]() ����
����
![]()
![]() ��
��
![]()
![]() ��
��![]() ֮��ĺ�������ʽΪ��
֮��ĺ�������ʽΪ��![]() ��xΪ��������
��x��������
��2����![]() ʱ��
ʱ��![]()
��![]() ��
��![]()
![]() ��
��![]() �����������
�����������
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
��ʱ����ͼ�����£��ڶԳ����Ҳ࣬![]() ��
��![]() �����������������
���������С��������![]() Ϊ������
������
![]() ��
��![]() ʱ��
ʱ��![]() Ԫ��
Ԫ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() �����
�����![]() Ԫ��
Ԫ��
����������![]()
��![]() ����������������Ϊ
����������������Ϊ![]() Ԫ��
Ԫ��
��3����![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]()
![]() ��
��
��![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
��
����������![]() Ԫ���ǵ�
Ԫ���ǵ�![]() ��
��![]() ��
��![]() �죮
�죮

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�����Ŀ��һ�����ѣ��˷�֧Ԯ�����¹ڷ��ס�������Ϯ������ҽ����Ա������ӧ��������ս���⣬�ڶ���ҵҲ���Ԯ��֮�֣�ij��˾�üף������ֻ������人���Ͱ������ʣ��������ص�����������±���
���ֻ������� | ���ֻ������� | �ϼ������ʶ��� | |
��һ�� | 3 | 4 | 29 |
�ڶ��� | 2 | 6 | 31 |
��1����ס������ֻ���ÿ�����طֱ���������ٶ����ʣ�
��2��Ŀǰ��46.4������Ҫ���䵽�人���ù�˾�ⰲ�ż��һ�����10����ȫ������һ�����꣬����ÿ���׳�һ�����ͻ���500Ԫ��ÿ���ҳ�һ�����ͻ���300Ԫ�����ʸù�˾Ӧ��ΰ��ų������ʡ���ã�