题目内容
(8分)如图:△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,G为垂足。
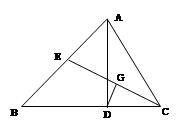
请说明下列结论成立的理由:
(1)DC=BE ; (2)∠B=2∠BCE 。

请说明下列结论成立的理由:
(1)DC=BE ; (2)∠B=2∠BCE 。
(1)如图:连DE
∵G是CE的中点,DG⊥CE,∴DG是CE的垂直平分线
∴ DE=DC
∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线
∴DE=BE=1/2AB ∴ DC=BE
(2)∵DE=DC ; ∴∠DEC=∠BCE ;
∴∠EDB=∠DEC+∠BCE=2∠BCE ;
∵DE=BE,∴∠B=∠EDB;∴∠B=2∠BCE

∵G是CE的中点,DG⊥CE,∴DG是CE的垂直平分线
∴ DE=DC
∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线
∴DE=BE=1/2AB ∴ DC=BE
(2)∵DE=DC ; ∴∠DEC=∠BCE ;
∴∠EDB=∠DEC+∠BCE=2∠BCE ;
∵DE=BE,∴∠B=∠EDB;∴∠B=2∠BCE
试题分析:解:
(1)如图:连DE

∵G是CE的中点,DG⊥CE,∴DG是CE的垂直平分线
∴ DE=DC
∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线
∴DE=BE=1/2AB ∴ DC=BE
(2)∵DE=DC ; ∴∠DEC=∠BCE ;
∴∠EDB=∠DEC+∠BCE=2∠BCE ;
∵DE=BE,∴∠B=∠EDB;∴∠B=2∠BCE
点评:本题难度中等,主要学生利用垂直平分线及直角斜边性质等来证明。

练习册系列答案
相关题目

 ,求△ABC的面积;
,求△ABC的面积; 的值.
的值.
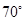 ,则其底角为 .
,则其底角为 .

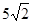 ,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是______。
,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是______。