题目内容
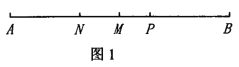
【题目】(1)如图1所示,已知线段AB=20cm,在AB上取一点P,M是AB的中点,N是AP中点,若MN=3cm,求线段AP的长;
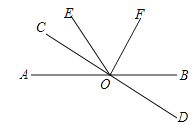
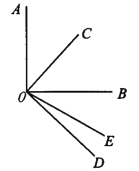
(2)如图2所示,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.则∠COE是多少度?
【答案】(1)14;(2)75°.
【解析】
(1)根据线段中点的定义和线段的和差即可得到结论;
(2)求出∠BOE的度数,根据角的和差关系即可得出答案.
解:(1)∵AB=20cm,M是AB的中点,
∴AM=![]() AB=
AB=![]() ×20=10cm,
×20=10cm,
∵MN=3cm,
∴AN=AM-MN=10-3=7cm,
∵N是AP中点,
∴AP=2AN=2×7=14.
(2))∵∠AOB=90°,OC平分∠AOB,
∴∠AOC=∠COB=![]() ∠AOB=45°,
∠AOB=45°,
∵∠COD=90°,
∴∠BOD=45°,
∵∠BOD=3∠DOE,
∴∠DOE=15°,
∴∠BOE=30°,
∴∠COE=∠COB+∠BOE=45°+30°=75°.

练习册系列答案
相关题目