题目内容
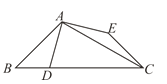
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
【答案】![]()
【解析】
过A点作BC的垂线,E点作AC的垂线,构造全等三角形,利用对应角相等计算得出∠DAM=15°,在AM上截取AG=DG,则∠DGM=30°,设DM=a,通过勾股定理可得到DG=AG=2a,GM=![]() a,AM=BM=(
a,AM=BM=(![]() ,BD=(
,BD=(![]() ,AB=
,AB=![]() (
(![]() ,代入计算即可.
,代入计算即可.
过A点作AM⊥BC于M点,过E点EN⊥AC于N点.
∵∠BCA=30°,AE=EC
∴AM=![]() AC,AN=
AC,AN=![]() AC
AC
∴AM=AN
又∵AD=AE
∴RtADM RtAEN(HL)
∴∠DAM=∠EAN
又∵∠MAC=60°,AD⊥AE
∴∠DAM=∠EAN=15°
在AM上截取AG=DG,则∠DGM=30°
设DM=a,则 DG=AG=2a,
根据勾股定理得:GM=![]() a,
a,
∵∠ABC=45°
∴AM=BM=(![]()
∴BD=(![]() ,AB=
,AB=![]() (
(![]() ,
,
∴![]()
故答案为:![]()


【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别 | 分数x | 频数 |
A | 40≤x<50 | 20 |
B | 50≤x<60 | 30 |
C | 60≤x<70 | 50 |
D | 70≤x<80 | m |
E | 80≤x<90 | 40 |
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数

【题目】甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
平均数 | 方差 | 中位数 | 众数 | 极差 | |
甲 | 75 | 75 | |||
乙 | 33.3 | 15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?