题目内容
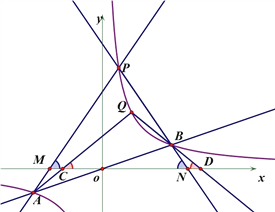
【题目】如图，反比例函数y＝
的图象与一次函数y＝
x的图象交于点A、B，点B的横坐标是4．点P是第一象限内反比例函数图象上的动点，且在直线AB的上方．
（1）若点P的坐标是（1，4），直接写出k的值和△PAB的面积；
（2）设直线PA、PB与x轴分别交于点M、N，求证：△PMN是等腰三角形；
（3）设点Q是反比例函数图象上位于P、B之间的动点（与点P、B不重合），连接AQ、BQ，比较∠PAQ与∠PBQ的大小，并说明理由．
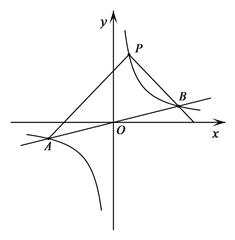
【答案】（1）k＝4，S△PAB＝15；（2）证明见解析；（3）∠PAQ＝∠PBQ.
【解析】试题分析：（1）根据题意求出B点的坐标，然后利用待定系数法可求k的值；
（2）过点P作PH⊥x轴于H，然后根据反比例函数的解析式设出P点的坐标，然后可得方程组，求出PA、PB的解析式，然后得含m、n的点M、N的坐标，然后根据线段垂直平分线的性质可求证；
（3）同（2）方法，利用等边对等角和三角形的外角可证.
试题解析：（1）根据B点的横坐标求出B点的 （4，1），
（3） 同理可证，QC=QD,
利用等边对等角和三角形的外角可证。如图。
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
