Question

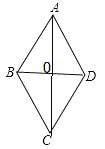
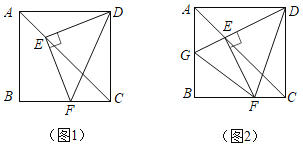
【题目】如图1，在正方形ABCD中，点E，F分别是AC，BC上的点，且满足DE⊥EF，垂足为点E，连接DF．

（1）求∠EDF= （填度数）；

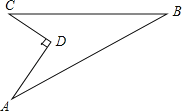
（2）延长DE交AB于点G，连接FG，如图2，猜想AG，GF，FC三者的数量关系，并给出证明；

（3）①若AB=6，G是AB的中点，求△BFG的面积；

②设AG=a，CF=b，△BFG的面积记为S，试确定S与a，b的关系，并说明理由．

Answer 1

【答案】(1)45°；(2)GF=AG+CF，证明见解析；(3)①6； ②，理由见解析.

【解析】

（1）如图1中，连接BE．利用全等三角形的性质证明EB=ED，再利用等角对等边证明EB=EF即可解决问题．

（2）猜想：GF=AG+CF．如图2中，将△CDF绕点D旋转90°，得△ADH，证明△GDH≌△GDF（SAS）即可解决问题．

（3）①设CF=x，则AH=x，BF=6-x，GF=3+x，利用勾股定理构建方程求出x即可．

②设正方形边长为x，利用勾股定理构建关系式，利用整体代入的思想解决问题即可．

解：（1）如图1中，连接BE．

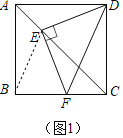
∵四边形ABCD是正方形，

∴CD=CB，∠ECD=∠ECB=45°，

∵EC=EC，

∴△ECB≌△ECD（SAS），

∴EB=ED，∠EBC=∠EDC，

∵∠DEF=∠DCF=90°，

∴∠EFC+∠EDC=180°，

∵∠EFB+∠EFC=180°，

∴∠EFB=∠EDC，

∴∠EBF=∠EFB，

∴EB=EF，

∴DE=EF，

∵∠DEF=90°，

∴∠EDF=45°

故答案为45°．

（2）猜想：GF=AG+CF．

如图2中，将△CDF绕点D旋转90°，得△ADH，

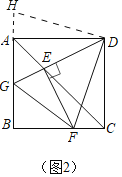
∴∠CDF=∠ADH，DF=DH，CF=AH，∠DAH=∠DCF=90°，

∵∠DAC=90°，

∴∠DAC+∠DAH=180°，

∴H、A、G三点共线，

∴GH=AG+AH=AG+CF，

∵∠EDF=45°，

∴∠CDF+∠ADG=45°，

∴∠ADH+∠ADG=45°

∴∠GDH=∠EDF=45°

又∵DG=DG

∴△GDH≌△GDF（SAS）

∴GH=GF，

∴GF=AG+CF．

（3）①设CF=x，则AH=x，BF=6-x，GF=3+x，

则有（3+x）2=（6-x）2+32，

解得x=2

∴S△BFG=BFBG=6．

②设正方形边长为x，

∵AG=a，CF=b，

∴BF=x-b，BG=x-a，GF=a+b，

则有（x-a）2+（x-b）2=（a+b）2，

化简得到：x2-ax-bx=ab，

∴S=（x-a）（x-b）=（x2-ax-bx+ab）=×2ab=ab．