题目内容
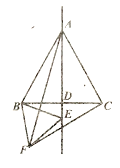
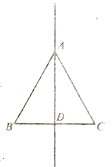
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点(0<AD<![]() AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
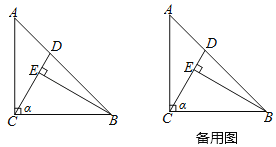
(1)①依题意补全图形.
②若α=60°,则∠CAF=_____°;![]() =_____;
=_____;
(2)用含α的式子表示EF与AB之间的数量关系,并证明.
【答案】(1)①补图见解析;②30,![]() ;(2)EF=ABcosα;证明见解析.
;(2)EF=ABcosα;证明见解析.
【解析】
(1)①利用旋转直接画出图形,
②先求出∠CBE=30°,再判断出△ACF≌△BCE,得出∠CAF=30°,再利用等腰直角三角形的性质计算即可得出结论;
(2)先判断出△ACF≌△BCE,得出∠CAF=α,再同(1)②的方法即可得出结论.
(1)①将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF,如图1;
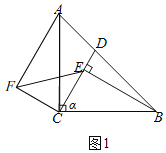
②∵BE⊥CD,∠CEB=90°,
∵α=60°,
∴∠CBE=30°,
在Rt△ABC中,AC=BC,
∴AC=![]() AB,
AB,
∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
在△ACF和△BCE中,
AC=BC,∠FCA=∠ECB,FC=EC,
∴△ACF≌△BCE(SAS),
∴∠AFC=∠BEC=90°,∠CAF=∠CBE=30°,
∴CF=![]() AC,
AC,
由旋转知,CF=CE,∠ECF=90°,
∴EF=![]() CF=
CF=![]() AC=
AC=![]() ×
×![]() AB=
AB=![]() AB,
AB,
∴![]() =
=![]() ,
,
故答案为30,![]() ;
;
(2)EF=ABcosα.
证明:∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
同(1)②的方法知,△ACF≌△BCE,
∴∠AFC=∠BEC=90°,
∴在Rt△AFC中,cos∠FCA=![]() .
.
∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°.
∵∠ECF=90°,CE=CF,
∴∠CFE=∠CEF=45°.
在△FCE和△ACB中,
∠FCE=∠ACB=90°,
∠CFE=∠CAB=45°,
∴△FCE∽△ACB,
∴![]() =cos∠FCA=cosα,
=cos∠FCA=cosα,
即EF=ABcosα.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案