题目内容
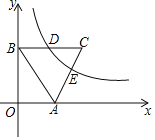
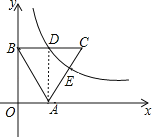
【题目】如图,在平面直角系中,点A在x轴正半轴上,点B在y轴正半轴上,∠ABO=30°,AB=2,以AB为边在第一象限内作等边△ABC,反比例函数的图象恰好经过边BC的中点D,边AC与反比例函数的图象交于点E.
(1)求反比例函数的解析式;
(2)求点E的横坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接利用等边三角形的性质结合举行的判定方法得出D点坐标进而得出答案;
(2)首先求出AC的解析式进而将两函数联立求出E点坐标即可.
解:(1)∵∠ABO=30°,AB=2,
∴OA=1,![]() ,
,
连接AD.
∵△ABC是等边三角形,点D是BC的中点,
∴AD⊥BC,
又∠OBD=∠BOA=90°,
∴四边形OBDA是矩形,
∴![]() ,
,
∴反比例函数解析式是![]() .
.
(2)由(1)可知,A(1,0),![]() ,
,
设一次函数解析式为y=kx+b,将A,C代入得 ,解得
,解得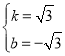 ,
,
∴![]() .
.
联立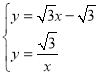 ,消去y,得
,消去y,得![]() ,
,
变形得x2﹣x﹣1=0,
解得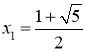 ,
,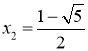 ,
,
∵xE>1,
∴![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?