题目内容
【题目】己知![]() 是等边三角形,
是等边三角形,![]() 于点
于点![]() ,点
,点![]() 是直线
是直线![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() ;
;
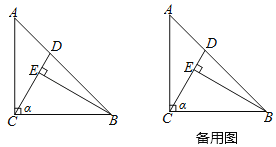
(1)如图1,当点![]() 在线段
在线段![]() 上时,猜想
上时,猜想![]() 和
和![]() 的数量关系;(直接写出结果)
的数量关系;(直接写出结果)
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点![]() 在直线
在直线![]() 上运动,当
上运动,当![]() 是等腰直角三角形时,请直接写出
是等腰直角三角形时,请直接写出![]() 的度数.
的度数.
图1 图2
图2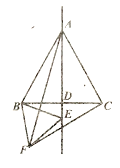 备用图
备用图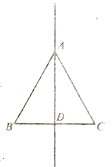
【答案】(1)∠AFC+∠FAC=90°;(2)成立,理由见解析;(3)15°或75°
【解析】
(1)由旋转的性质可得,![]() ,
,![]() ,由“SAS”可证△ABE≌△CBF,可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
,由“SAS”可证△ABE≌△CBF,可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
(2)由旋转的性质可得,![]() ,
,![]() ,先求证△ABE≌△CBF,由△ABE和△CBF全等可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
,先求证△ABE≌△CBF,由△ABE和△CBF全等可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
(3)由全等三角形的性质和等边三角形的性质可得AB=AE,由等腰三角形的性质求解即可;
解:
(1)∠AFC+∠FAC=90°,
理由如下:连接AF,
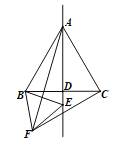
∵![]() 是等边三角形,
是等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°,
∵AB=AC,AD⊥BC,
∴∠BAD=30°,
∵将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,
,
∴∠EBF=∠ABC=60°,
∴∠ABC=∠EBF=60°,
∴∠ABE=∠FBC,且AB=AC,![]() ,
,
∴△ABE≌△CBF,
∴∠BAE=∠BCF=30°,
∴∠ACF=90°,
即∠AFC+∠FAC=90°;
(2)成立,∠AFC+∠FAC=90°,
证明:由旋转可得,
∠EBF=60°,BE=BF,
∴△BEF是等边三角形,
∵△ABC是等边三角形,
∴AB=BC,∠BAC=∠ABC=∠ACB=60°,
∴∠ABC=∠EBF=60°,
∴∠ABC+∠CBE=∠EBF+∠CBE,
即∠ABE=∠CBF,
∴△ABE≌△CBF,
∴∠BAE=∠BCF,
∵AD⊥BC,
∴∠BAE=![]() ∠BAC=30°,
∠BAC=30°,
∴∠BCF=30°,
∴∠ACB+∠BCF=90°,
即∠ACF=90°,
∴∠AFC+∠FAC=90°,

(3)∵△ACF是等腰直角三角形,
∴AC=CF,
∵△ABE≌△CBF,
∴CF=AE,
∴AC= AE=AB,
∴![]() ,
,
∴![]() ,
,