题目内容
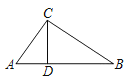
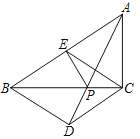
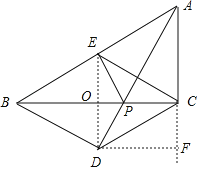
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点E是斜边AB上的一个动点,连接CE,过点B,C分别作BD∥CE,CD∥BE,BD与CD相交于点D.
(1)当CE⊥AB时,求证:四边形BECD是矩形;
(2)填空:
①当BE的长为______时,四边形BECD是菱形;
②在①的结论下,若点P是BC上一动点,连接AP,EP,则AP+EP的最小值为______.
【答案】(1)证明见解析;(2)①![]() ;②3
;②3![]() .
.
【解析】
(1)根据矩形的判定:有一个角是直角的平行四边形是矩形即可证明;
(2)①根据菱形的判定定理:对角线互相垂直的平行四边形是菱形即可求解;
②根据对称性:连接ED交BC于点P,此时AP+EP=AD,最小,再过点D作DF垂直AC的延长线于点F,根据勾股定理即可求解.
如图所示:
(1)∵BD∥CE,CD∥BE,
∴四边形BDCE是平行四边形,
∵CE⊥AB,
∴∠BEC=90°,
∴四边形BECD是矩形;
(2)①当BE的长为![]() 时,四边形BECD是菱形.理由如下:
时,四边形BECD是菱形.理由如下:
连接ED,与BC交于点O,
∵四边形BDCE是平行四边形,
当BC和DE互相垂直平分时,四边形BDCE是菱形,
BO=![]() BC=3,OE=
BC=3,OE=![]() AC=2,
AC=2,
∴根据勾股定理,得
BE=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.
②连接AD,与BC交于点P,连接PE,
此时PD=PE,AP+EP最小,
∴AP+PE=AP+PD=AD,
过点D作DF垂直于AC的延长线于点F,
得矩形ODFC,
∴CF=OD=2,DF=OC=3,
∴AF=AC+CF=6,
∴在Rt△ADF中,根据勾股定理,得
AD=![]() =
=![]() =3
=3![]() .
.
∴AP+EP的最小值为3![]() .
.
故答案为3![]() .
.

练习册系列答案
相关题目