题目内容
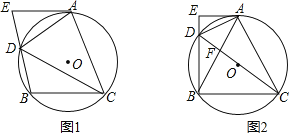
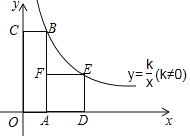
【题目】如图，在平面直角坐标系内，四边形OABC是矩形，四边形ADEF是正方形，点A，D在x轴的正半轴上，点F在BA上，点B、E均在反比例函数y＝
（k≠0）的图象上，若点B的坐标为(1，6)，则正方形ADEF的边长为（ ）
A.1B.2C.4D.6
【答案】B
【解析】
由点B的坐标利用反比例函数图象上点的坐标特征即可求出k值，设正方形ADEF的边长为a，由此即可表示出点E的坐标，再根据反比例函数图象上点的坐标特征即可得出关于a的一元二次方程，解之即可得出结论．
∵点B的坐标为(1，6)，反比例函数y
的图象过点B，
∴k=1×6=6．
设正方形ADEF的边长为a(a＞0)，
则点E的坐标为(1+a，a)．
∵反比例函数y的图象过点E，
∴a(1+a)=6，
解得：a=2或a=﹣3(舍去)，
∴正方形ADEF的边长为2．
故选：B．
练习册系列答案
相关题目
【题目】汛期到来，山洪暴发．下表记录了某水库
内水位的变化情况，其中
表示时间(单位：
)，
表示水位高度(单位：
)，当
时，达到警戒水位，开始开闸放水．
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |
(1)在给出的平面直角坐标系中，根据表格中的数据描出相应的点．
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式．
(3)据估计，开闸放水后，水位的这种变化规律还会持续一段时间，预测何时水位达到
．
