题目内容
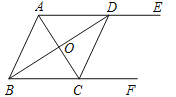
【题目】如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为_______.

【答案】![]()
【解析】
如图,作OH⊥CD于H,连结OC,根据垂径定理得HC=HD,由题意得OA=4,即OP=2,在Rt△OPH中,根据含30°的直角三角形的性质计算出OH=![]() OP=1,然后在在Rt△OHC中,利用勾股定理计算得到CH=
OP=1,然后在在Rt△OHC中,利用勾股定理计算得到CH=![]() ,即CD=2CH=2
,即CD=2CH=2![]() .
.
 解:如图,作OH⊥CD于H,连结OC,
解:如图,作OH⊥CD于H,连结OC,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,
∵∠OPH=30°,
∴∠POH=60°,
∴OH=![]() OP=1,
OP=1,
在Rt△OHC中,
∵OC=4,OH=1,
∴CH=![]() ,
,
∴CD=2CH=2![]() .
.
故答案为2![]() .
.

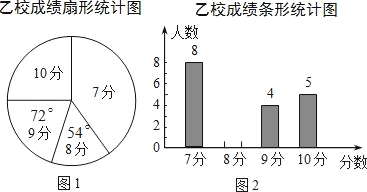
【题目】(10分)甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 |
| 8 |
(1)请将甲校成绩统计表和图2的统计图补充完整;
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
【题目】甲乙两个仓库要向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)(本题满分10分)
路程/千米 | 运费(元/吨、千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A地 | 20 | 15 | 12 | 12 |
B地 | 25 | 20 | 10 | 8 |
(1)设甲库运往A地水泥![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?