题目内容
【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为_____.
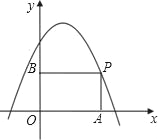
【答案】6
【解析】∵y=﹣x2+x+2,
∴当y=0时,﹣x2+x+2=0即﹣(x﹣2)(x+1)=0,
解得 x=2或x=﹣1
故设P(x,y)(2>x>0,y>0),
∴C=2(x+y)=2(x﹣x2+x+2)=﹣2(x﹣1)2+6.
∴当x=1时,C最大值=6,.
即:四边形OAPB周长的最大值为6.
点睛 :本题主要考查二次函数的最值以及二次函数图象上点的坐标特征.设P(x,y)(2>x>0,y>0),根据矩形的周长公式得到C=﹣2(x﹣1)2+6.最后根据根据二次函数的性质来求最值是关键.

练习册系列答案
相关题目