ΧβΡΩΡΎ»ί
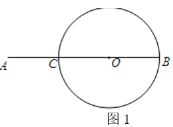
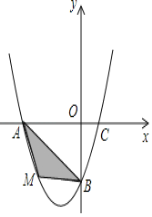
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷Σ≈ΉΈοœΏΨ≠ΙΐA(©¹2Θ§0)Θ§B(0Θ§©¹2)Θ§C(1Θ§0)»ΐΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΒψMΈΣΒΎ»ΐœσœόΡΎ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΒψMΒΡΚαΉχ±ξΈΣmΘ§ΓςAMBΒΡΟφΜΐΈΣSΘ§«σSΙΊ”ΎmΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωSΒΡΉν¥σ÷ΒΘΜ
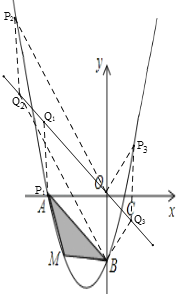
Θ®3Θ©»τΒψP «≈ΉΈοœΏ…œΒΡΕ·ΒψΘ§ΒψQ «÷±œΏyΘΫ©¹x…œΒΡΕ·ΒψΘ§≈–Εœ”–ΦΗΗωΈΜ÷ΟΡήΙΜ ΙΒΟΒψPΓΔQΓΔBΓΔOΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΤΫ––ΥΡ±Ώ–ΈΘ§÷±Ϋ”–¥≥ωœύ”ΠΒΡΒψQΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫx2+x©¹2ΘΜΘ®2Θ©SΘΫ©¹m2©¹2mΘ®©¹2ΘΦmΘΦ0Θ©Θ§SΒΡΉν¥σ÷ΒΈΣ1ΘΜΘ®3Θ©ΒψQΉχ±ξΈΣΘΚ(©¹2Θ§2)Μρ(©¹1+![]() Θ§1©¹
Θ§1©¹![]() )Μρ(©¹1©¹
)Μρ(©¹1©¹![]() Θ§1+
Θ§1+![]() )Μρ(2Θ§©¹2)Θ°
)Μρ(2Θ§©¹2)Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…η¥Υ≈ΉΈοœΏΒΡΚ· ΐΫβΈω ΫΈΣΘΚyΘΫax2+bx+cΘ§ΫΪAΘ§BΘ§C»ΐΒψ¥ζ»κyΘΫax2+bx+cΘ§Ν–ΖΫ≥ΧΉι«σ≥ωaΓΔbΓΔcΒΡ÷ΒΦ¥Ω…ΒΟ¥πΑΗΘΜ
Θ®2Θ©»γΆΦ1Θ§ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΫΜAB”ΎΒψDΘ§MΒψΒΡΚαΉχ±ξΈΣmΘ§«“ΒψM‘ΎΒΎ»ΐœσœόΒΡ≈ΉΈοœΏ…œΘ§…ηMΒψΒΡΉχ±ξΈΣΘ®mΘ§m2+m©¹2Θ©Θ§©¹2ΘΦmΘΦ0Θ§”…AΓΔBΉχ±ξΩ…«σ≥ω÷±œΏABΒΡΫβΈω ΫΈΣyΘΫ©¹x©¹2Θ§‘ρΒψDΒΡΉχ±ξΈΣΘ®mΘ§©¹m©¹2Θ©Θ§Φ¥Ω…«σ≥ωMDΒΡ≥ΛΕ»Θ§Ϋχ“Μ≤Ϋ«σ≥ωΓςMABΒΡΟφΜΐSΙΊ”ΎmΒΡΚ· ΐΙΊœΒ ΫΘ§ΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ Φ¥Ω…«σ≥ωΤδΉν¥σ÷ΒΘΜ
Θ®3Θ©…ηPΘ®xΘ§x2+x©¹2Θ©Θ§Ζ÷«ιΩωΧ÷¬έΘ§ΔΌΒ±OBΈΣ±Ώ ±Θ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ÷ΣPQΓΈOBΘ§«“PQΘΫOBΘ§‘ρQΘ®xΘ§©¹xΘ©Θ§Ω…Ν–≥ωΙΊ”ΎxΒΡΖΫ≥ΧΘ§Φ¥Ω…«σ≥ωΒψQΒΡΉχ±ξΘΜΔΎΒ±BOΈΣΕ‘Ϋ«œΏ ±Θ§OQΓΈBPΘ§A”κP”ΠΗΟ÷ΊΚœΘ§OPΘΫ2Θ§ΥΡ±Ώ–ΈPBQOΈΣΤΫ––ΥΡ±Ώ–ΈΘ§‘ρBQΘΫOPΘΫ2Θ§QΚαΉχ±ξΈΣ2Θ§Φ¥Ω…–¥≥ωΒψQΒΡΉχ±ξΘ°
Θ®1Θ©…η¥Υ≈ΉΈοœΏΒΡΚ· ΐΫβΈω ΫΈΣΘΚyΘΫax2+bx+cΘ§
ΫΪAΘ®©¹2Θ§0Θ©Θ§BΘ®0Θ§©¹2Θ©Θ§CΘ®1Θ§0Θ©»ΐΒψ¥ζ»κΘ§ΒΟ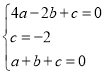 Θ§
Θ§
ΫβΒΟΘΚ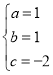 Θ§
Θ§
Γύ¥ΥΚ· ΐΫβΈω ΫΈΣΘΚyΘΫx2+x©¹2Θ°
Θ®2Θ©»γΆΦΘ§ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΫΜAB”ΎΒψDΘ§
ΓΏMΒψΒΡΚαΉχ±ξΈΣmΘ§«“ΒψM‘ΎΒΎ»ΐœσœόΒΡ≈ΉΈοœΏ…œΘ§
Γύ…ηMΒψΒΡΉχ±ξΈΣΘ®mΘ§m2+m©¹2Θ©Θ§©¹2ΘΦmΘΦ0Θ§
…η÷±œΏABΒΡΫβΈω ΫΈΣyΘΫkx©¹2Θ§
Α―AΘ®©¹2Θ§0Θ©¥ζ»κΒΟΘ§-2k-2=0Θ§
ΫβΒΟΘΚkΘΫ©¹1Θ§
Γύ÷±œΏABΒΡΫβΈω ΫΈΣyΘΫ©¹x©¹2Θ§
ΓΏMDΓΈy÷αΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®mΘ§©¹m©¹2Θ©Θ§
ΓύMDΘΫ©¹m©¹2©¹Θ®m2+m©¹2Θ©ΘΫ©¹m2©¹2mΘ§
ΓύSΓςMABΘΫSΓςMDA+SΓςMDB
ΘΫ![]() MDOA
MDOA
ΘΫ![]() ΓΝ2Θ®m2©¹2mΘ©
ΓΝ2Θ®m2©¹2mΘ©
ΘΫ©¹m2©¹2m
ΘΫ©¹Θ®
ΓΏ©¹2ΘΦmΘΦ0Θ§
ΓύΒ±mΘΫ©¹1 ±Θ§SΓςMAB”–Ήν¥σ÷Β1Θ§
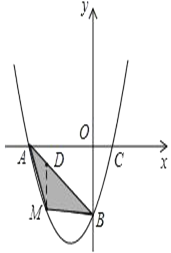
Ήέ…œΥυ ωΘ§SΙΊ”ΎmΒΡΚ· ΐΙΊœΒ Ϋ «SΘΫ©¹m2©¹2mΘ®©¹2ΘΦmΘΦ0Θ©Θ§SΒΡΉν¥σ÷ΒΈΣ1Θ°
Θ®3Θ©…ηPΘ®xΘ§x2+x©¹2Θ©Θ§
ΔΌ»γΆΦΘ§Β±OBΈΣ±Ώ ±Θ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ÷ΣPQΓΈOBΘ§«“PQΘΫOBΘ§
ΓύQΒΡΚαΉχ±ξΒ»”ΎPΒΡΚαΉχ±ξΘ§
ΓΏ÷±œΏΒΡΫβΈω ΫΈΣyΘΫ©¹xΘ§
‘ρQΘ®xΘ§©¹xΘ©Θ§
”…PQΘΫOBΘ§ΒΟ|©¹x©¹Θ®x2+x©¹2Θ©|ΘΫ2Θ§
Φ¥|©¹x2©¹2x+2|ΘΫ2Θ§
Β±©¹x2©¹2x+2ΘΫ2 ±Θ§x1ΘΫ0Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§x2ΘΫ©¹2Θ§
ΓύQΘ®©¹2Θ§2Θ©Θ§
Β±©¹x2©¹2x+2ΘΫ©¹2 ±Θ§x1ΘΫ©¹1+![]() Θ§x2ΘΫ©¹1©¹
Θ§x2ΘΫ©¹1©¹![]() Θ§
Θ§
ΓύQΘ®©¹1+![]() Θ§1©¹
Θ§1©¹![]() Θ©ΜρΘ®©¹1©¹
Θ©ΜρΘ®©¹1©¹![]() Θ§1+
Θ§1+![]() Θ©Θ§
Θ©Θ§
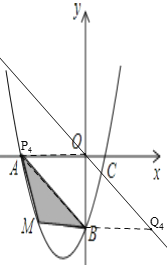
ΔΎ»γΆΦΘ§Β±BOΈΣΕ‘Ϋ«œΏ ±Θ§OQΓΈBPΘ§
ΓΏ÷±œΏABΒΡΫβΈω ΫΈΣy=-x-2Θ§÷±œΏOQΒΡΫβΈω ΫΈΣy=-xΘ§
ΓύA”κP÷ΊΚœΘ§OPΘΫ2Θ§ΥΡ±Ώ–ΈPBQOΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύBQΘΫOPΘΫ2Θ§ΒψQΒΡΚαΉχ±ξΈΣ2Θ§
Α―x=2¥ζ»κyΘΫ©¹xΒΟy=-2Θ§
ΓύQΘ®2Θ§©¹2Θ©Θ§
Ήέ…œΥυ ωΘ§ΒψQΒΡΉχ±ξΈΣΘ®©¹2Θ§2Θ©ΜρΘ®©¹1+![]() Θ§1©¹
Θ§1©¹![]() Θ©ΜρΘ®©¹1©¹
Θ©ΜρΘ®©¹1©¹![]() Θ§1+
Θ§1+![]() Θ©ΜρΘ®2Θ§©¹2Θ©Θ°
Θ©ΜρΘ®2Θ§©¹2Θ©Θ°

ΓΨΧβΡΩΓΩ¥”ΦΉΒΊΒΫ““ΒΊ”–AΘ§BΘ§C»ΐΧθ≤ΜΆ§ΒΡΙΪΫΜœΏ¬ΖΘ°ΈΣΝΥΫβ‘γΗΏΖεΤΎΦδ’β»ΐΧθœΏ¬Ζ…œΒΡΙΪΫΜ≥Β¥”ΦΉΒΊΒΫ““ΒΊΒΡ”Ο ±«ιΩωΘ§‘ΎΟΩΧθœΏ¬Ζ…œΥφΜζ―Γ»ΓΝΥ500ΗωΑύ¥ΈΒΡΙΪΫΜ≥ΒΘ§ ’Φ·ΝΥ’β–©Αύ¥ΈΒΡΙΪΫΜ≥Β”Ο ±Θ®ΒΞΈΜΘΚΖ÷÷”Θ©ΒΡ ΐΨίΘ§Ά≥ΦΤ»γœ¬ΘΚ
ΙΪΫΜ≥Β”Ο ± ΙΪΫΜ≥Β”Ο ±ΒΡΤΒ ΐ œΏ¬Ζ |
|
|
|
| ΚœΦΤ |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
‘γΗΏΖεΤΎΦδΘ§≥ΥΉχ_________Θ®ΧνΓΑAΓ±Θ§ΓΑBΓ±ΜρΓΑCΓ±Θ©œΏ¬Ζ…œΒΡΙΪΫΜ≥ΒΘ§¥”ΦΉΒΊΒΫ““ΒΊΓΑ”Ο ±≤Μ≥§Ιΐ45Ζ÷÷”Γ±ΒΡΩ…Ρή–‘Ήν¥σΘ°