Question

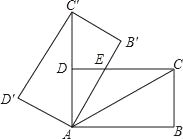
【题目】如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC′的中点恰好与D点重合，AB′交CD于点E．若AB=6，则△AEC的面积为_____．

Answer 1

【答案】4

【解析】分析：根据旋转后AC的中点恰好与D点重合，利用旋转的性质得到直角三角形ACD中，∠ACD=30°，再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°，进而得到∠EAC=∠ECA，利用等角对等边得到AE=CE，设AE=CE=x，表示出AD与DE，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出EC的长，即可求出三角形AEC面积．

详解：∵旋转后AC的中点恰好与D点重合，即AD=AC′=AC，

∴在Rt△ACD中，∠ACD=30°，即∠DAC=60°，

∴∠DAD′=60°，∴∠DAE=30°，

∴∠EAC=∠ACD=30°，∴AE=CE．

在Rt△ADE中，设AE=EC=x，

则有DE=DC﹣EC=AB﹣EC=6﹣x，AD=×6=2，

根据勾股定理得：x2=（6﹣x）2+（2）2，

解得：x=4，∴EC=4，

则S△AEC=ECAD=4．

故答案为：4．