题目内容
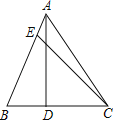
【题目】如图,在△ABC中,AD⊥BC于点D,点E在AB边上,连接CE,若∠BCE=2∠BAD,BE=2BD,AE:CD=3:8,S△ABC=39,则AC边的长为_____.
【答案】2![]()
【解析】
如图,在CD上截取DF=BD,由“AAS”可证△ABF≌△CBE,可得AB=BC=AF=CE,由勾股定理和三角形面积公式可求AD,CD的长,由勾股定理可求AC的长.
解:如图,在CD上截取DF=BD,
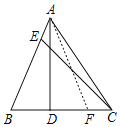
∵DF=BD,AD⊥BC,
∴AB=AF,且AD⊥BC,
∴∠BAF=2∠BAD,且∠BCE=2∠BAD,
∴∠BAF=∠BCE,且∠B=∠B,BF=2BD=BE,
∴△ABF≌△CBE(AAS)
∴AB=BC=AF=CE,
∴AE+BE=BD+CD,
∵AE:CD=3:8,
∴设AE=3x,CD=8x,
∴3x+2BD=BD+8x,
∴BD=5x,
∴AB=BC=13x,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:2![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目