题目内容
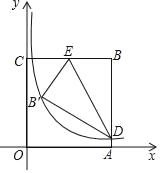
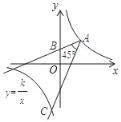
【题目】如图:双曲线![]() 经过点A(2,3),射线AB经过点B(0,2),将射线AB绕A按逆时针方向旋转45°,交双曲线于点C,则点C的坐标的为____.
经过点A(2,3),射线AB经过点B(0,2),将射线AB绕A按逆时针方向旋转45°,交双曲线于点C,则点C的坐标的为____.
【答案】(﹣1,﹣6).
【解析】
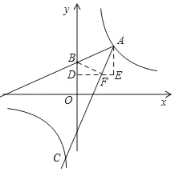
过B作BF⊥AC于F,过F作FD⊥y轴于D,过A作AE⊥DF于E,则△ABF为等腰直角三角形,易得△AEF≌△FDB,设BD=a,则EF=a,进一步得到DF=2-a=AE,OD=OB-BD=2-a,根据AE+OD=3,列出2-a+2-a=3,求得a的值,即可求得F的坐标,根据待定系数法求得直线AF的解析式,然后和反比例函数的解析式联立方程,解方程即可求得.
如图,过B作BF⊥AC于F,过F作FD⊥y轴于D,过A作AE⊥DF于E,则△ABF为等腰直角三角形,易得△AEF≌△FDB,设BD=a,则EF=a,
∵点A(2,3)和点B(0,2),
∴DF=2﹣a=AE,OD=OB﹣BD=2﹣a,
∵AE+OD=3,
∴2﹣a+2﹣a=3,
解得a=![]() ,
,
∴F(![]() ,
,![]() ),
),
设直线AF的解析式为y=kx+b,则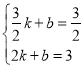 ,解
,解![]() ,
,
∴直线AF的解析式为y=3x﹣3,
∵双曲线![]() 经过点A(2,3),
经过点A(2,3),
∴k=2×3=6,
∴双曲线为y=![]() ,
,
解方程组 ,可得
,可得![]() 或
或![]() ,
,
∴C(﹣1,﹣6),
故答案为:(﹣1,﹣6).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目