题目内容
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
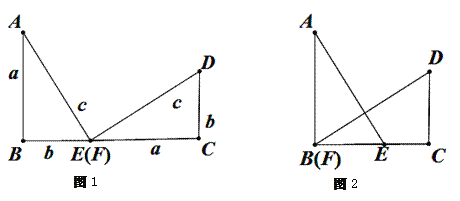
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
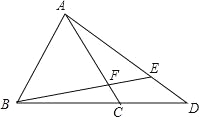
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;(2)p=﹣
x﹣1;(2)p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,当t=2时,p有最大值
,当t=2时,p有最大值![]() .(3)“落点”的个数有4个,点A1坐标为(
.(3)“落点”的个数有4个,点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).
【解析】
试题分析:(1)把点B的坐标代入直线解析式求出m的值,再把点C的坐标代入直线求解即可得到n的值,然后利用待定系数法求二次函数解析式解答;(2)令y=0求出点A的坐标,从而得到OA、OB的长度,利用勾股定理列式求出AB的长,然后根据两直线平行,内错角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根据矩形的周长公式表示出p,利用直线和抛物线的解析式表示DE的长,整理即可得到P与t的关系式,再利用二次函数的最值问题解答;(3)根据逆时针旋转角为90°可得A1O1∥y轴时,B1O1∥x轴,旋转角是180°判断出A1O1在x轴上,B1O1∥y轴,根据B1纵坐标为1,求出B1横坐标即可解决问题.
试题解析:(1)∵直线l:y=![]() x+m经过点B(0,﹣1),
x+m经过点B(0,﹣1),
∴m=﹣1,
∴直线l的解析式为y=![]() x﹣1,
x﹣1,
∵直线l:y=![]() x﹣1经过点C(4,n),
x﹣1经过点C(4,n),
∴n=![]() ×4﹣1=2,
×4﹣1=2,
∵抛物线y=![]() x2+bx+c经过点C(4,2)和点B(0,﹣1),
x2+bx+c经过点C(4,2)和点B(0,﹣1),
∴ ,
,
解得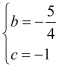 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;
x﹣1;
(2)令y=0,则![]() x﹣1=0,
x﹣1=0,
解得x=![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=![]() ,
,
在Rt△OAB中,OB=1,
∴AB=![]() =
=![]() ,
,
∵DE∥y轴,
∴∠ABO=∠DEF,
在矩形DFEG中,EF=DEcos∠DEF=DE![]() =
=![]() DE,
DE,
DF=DEsin∠DEF=DE![]() =
=![]() DE,
DE,
∴p=2(DF+EF)=2(![]() +
+![]() )DE=
)DE=![]() DE,
DE,
∵点D的横坐标为t(0<t<4),
∴D(t,![]() t2﹣
t2﹣![]() t﹣1),E(t,
t﹣1),E(t,![]() t﹣1),
t﹣1),
∴DE=(![]() t﹣1)﹣(
t﹣1)﹣(![]() t2﹣
t2﹣![]() t﹣1)=﹣
t﹣1)=﹣![]() t2+2t,
t2+2t,
∴p=![]() ×(﹣
×(﹣![]() t2+2t)=﹣
t2+2t)=﹣![]() t2+
t2+![]() t,
t,
∵p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,且﹣
,且﹣![]() <0,
<0,
∴当t=2时,p有最大值![]() .
.
(3)“落点”的个数有4个,如图1,图2,图3,图4所示.
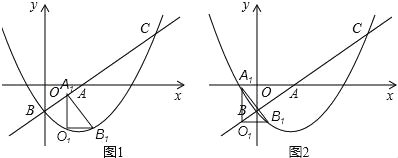
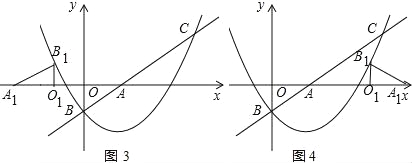
如图3,图4中,B1O1=BO=1,则![]() x2﹣
x2﹣![]() x﹣1=1,解得x=
x﹣1=1,解得x=![]() ,
,
∵A1O1=![]() ,
,
∴图3中,OA1=OO1+A1O1═![]() ,图4中OA1═OO1+O1A1=
,图4中OA1═OO1+O1A1=![]()
∴点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).

【题目】五位学生的一分钟跳绳成绩分布为(单位:个):126,134,134,135,160,在统计数据时,把其中一个134写出了124,则计算结果不受影响的是( )
A.中位数B.众数C.方差D.平均数
【题目】郑州市雾霾天气趋于严重,丹尼斯商场根据民众健康需要,代理销售每台 进价分别为600元、560元的A、B两种型号的空气净化器,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 4台 | 5台 | 7100元 |
第二周 | 6台 | 10台 | 12600元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的空气净化器的销售单价;
(2)若商场准备用不多于17200元的金额再采购这两种型号的空气净化器共30台,超市销售完这30台空气净化器能否实现利润为6200元的目标,若能,请给出相应的采购方案;若不能,请说明理由.