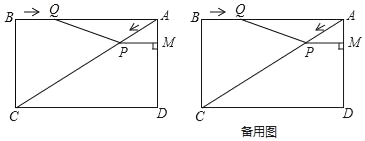
��Ŀ����
����Ŀ����֪��������y=x2+(2m��1)x��2m(��![]() <m��
<m��![]() )��ֱ��l�Ľ���ʽΪy=(k��1)x+2m��k+2.
)��ֱ��l�Ľ���ʽΪy=(k��1)x+2m��k+2.
(1)����������y�ύ���������Ϊ��3�����������ߵĶ������ꣻ
(2)��֤������������ֱ��l�����������㣻
(3)�������߾�����(x0����4)���Ҷ�������ʵ��x������ʽx2+(2m��1)x��2m����4�������� ��k��2��x��kʱ�������ߵ���СֵΪ2k+1. ��ֱ��l�Ľ���ʽ.
���𰸡���1��y=x2+2x��3������(��1����4)����2�������������3��y =��3 x +7��y =(1+2![]() )x +3+2
)x +3+2![]()
��������
��1������������y�ύ���������Ϊ��3�����m��ֵ���ٰ������ߵĽ���ʽ�����䷽���ɵõ������ߵĶ������ꣻ
��2��������������ֱ�ߵķ���������֤���䷽����������ͬ�ĸ�������0���ɣ�
��3���������֪y��Сֵ=��4�����m��![]() ����ʱ�����ߵĶԳ���Ϊֱ�� x����1���ٷ����������Ϻ�����ͼ�����k��ֵ���ɵó�����.
����ʱ�����ߵĶԳ���Ϊֱ�� x����1���ٷ����������Ϻ�����ͼ�����k��ֵ���ɵó�����.
��1���ߣ�2m=-3,
��2m=3��
�������ߣ�y= x2+(2m��1)x��2m =x2+2x��3=( x +1)2��4��
�ඥ������Ϊ��(��1����4)
��2�������ߣ�y=x2+(2m��1)x��2m
ֱ�ߣ�y=(k��1)x+2m��k+2.
x2+(2m��k)x��4m+k��2=0
��=(2m��k)2��4(��4m+k��2)= (2m��k)2+16m��4k+8
��(2m��k)2+4(2m��k)+8m+4
=(2m��k+2)2+8m+4
��m>��![]() �� (2m��k+2)2��0
�� (2m��k+2)2��0
���>0����������ֱ��l������������.
��3���������֪y��Сֵ=��4
����![]() =��4��m��
=��4��m��![]() ��m����
��m����![]()
�ߣ�![]() <m��
<m��![]()
��m��![]() ����ʱ�����ߵĶԳ���Ϊֱ�� x����1
����ʱ�����ߵĶԳ���Ϊֱ�� x����1
�ٵ�k����1ʱ����������k��2��x��k�ϣ�ͼ���½���y��x�������С.
��ʱy��Сֵ= k2+2k��3
�� k2+2k��3=2k+1
��ã�k1��2>��1����ȥ����k2����2
�ڵ�k��2<��1<k����<��1<k <1ʱ����������k��2��x��k�ϣ� y��Сֵ=��4
�� 2k+1=��4
���ã�k=��![]() <��1 (��ȥ)��
<��1 (��ȥ)��
�۵�k��2����1����k��1ʱ����������k��2��x��k�ϣ�ͼ��������![]() ��
��![]() ���������
���������
��ʱy��Сֵ= (k��2)2+2 (k��2)��3
(k��2)2+2 (k��2)��3=2k+1��
��ã�k1��2+2![]() ��k2��2��2
��k2��2��2![]() <1 (��ȥ)��
<1 (��ȥ)��
����������ֱ��![]() ��y =��3 x +7��y =(1+2
��y =��3 x +7��y =(1+2![]() )x +3+2
)x +3+2![]()